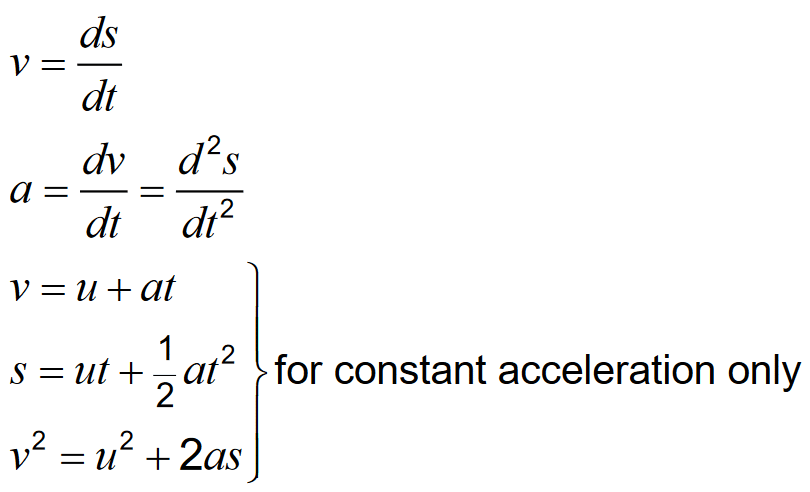Advanced Higher Physics

Kinematics - Linear Motion

Derivation of linear equations of motion

We start by defining acceleration:
Acceleration = change in velocity divided by the change in time
in equation form: $a = \frac{Δv}{Δt}$

When the time change is long we get an average acceleration. What we wish to do is make the time change as short as possible in order to determine an instantaneous velocity change and therefore an instantaneous acceleration.
Acceleration can be defined as $a = \frac{dv}{dt}$

Integrate with respect to time: $\int a = \int \frac{dv}{dt} dt = \int a dt$ $a \int_{0}^{t} dt = \int_{u}^{v} dv$ $a \int_{0}^{t} dt = \int_{u}^{v} dv$ $a 0_{t} [t] = \int_{u}^{v} dv$

Mandatory Course Key Areas - Aug 2018

Kinematic relationships

Knowledge that differential calculus notation is used to represent rate of change.

Knowledge that velocity is the rate of change of displacement with time, acceleration is the rate of change of velocity with time, and acceleration is the second differential of displacement with time.

Derivation of the equations of motion

v = u + at

and

s = ut + \frac{1}{2} {at}^{2}

using calculus methods

Use of calculus methods to calculate instantaneous displacement, velocity, and acceleration for straight line motion with a constant or varying acceleration.

Use of appropriate relationships to carry out calculations involving displacement, velocity, acceleration, and time for straight line motion with constant or varying acceleration.

SUVAT Equations in AH physics with constant acceleration

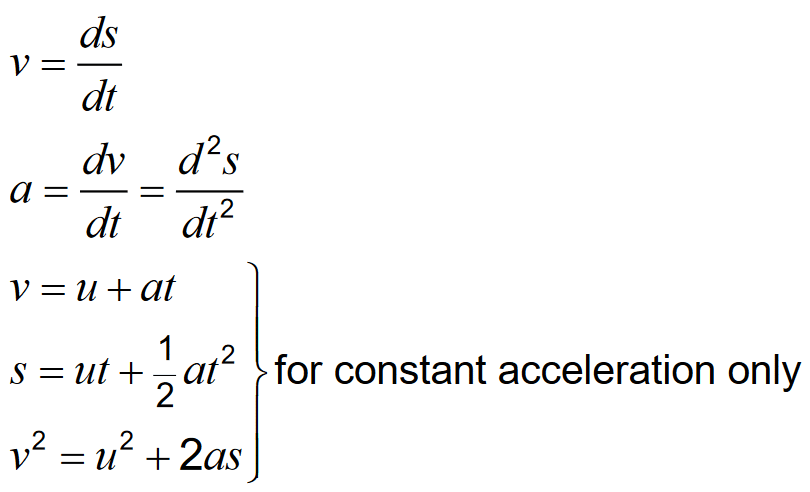
Knowledge that the gradient of a curve (or a straight line) on a motion–time graph represents instantaneous rate of change, and can be found by differentiation.

Knowledge that the gradient of a curve (or a straight line) on a displacement–time graph is the instantaneous velocity, and that the gradient of a curve (or a straight line) on a velocity–time graph is the instantaneous acceleration.

Knowledge that the area under a line on a graph can be found by integration.

Knowledge that the area under an acceleration–time graph between limits is the change in velocity, and that the area under a velocity–time graph between limits is the displacement.

Determination of displacement, velocity or acceleration by the calculation of the gradient of the line on a graph or the calculation of the area under the line between limits on a graph.

Advanced Higher Physics

Topics

Kinematics - Linear Motion

Derivation of linear equations of motion

Mandatory Course Key Areas - Aug 2018