Refraction of light
When light passes from air to water or from air to another material it gets slowed down. This is because the density of the material is greater than the density of air. The frequency with which the waves move through the material is the same as the frequency in air.
It is also possible to see water waves slowed down as they pass from a region of deep water to one of shallow water. This change of speed of a wave while maintaining frequency is called refraction.
Remember that wave speed, frequency and wavelength are related using the following formula:
Since the wave speed has slowed down and the frequency is unchanged, the wavelength must change. The wavelength of the light in glass or water must be less than its wavelength in air.
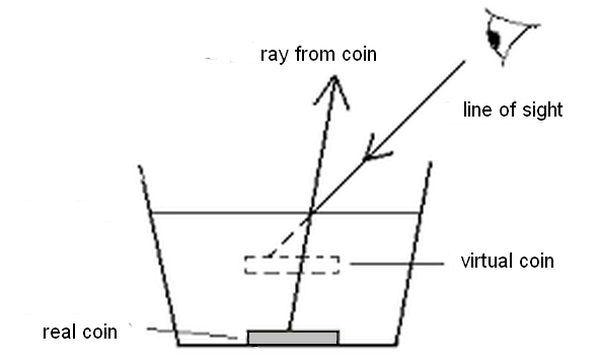
One of the most noticable effects of refraction is the change of direction of light when it passes from one medium to another. This is used to make a coin below a glass disappear when the glass is filled with water.

You may also have noticed pencils look broken, or things look higher up in the water than they really are.
Change of Direction
Before we look at an experiment there are a few terms which must be described:
- ray: A stream of light moving along a straight line
- normal: An imaginary line drawn at 90° to the surface where a ray meets the surface. This is the line which all angles are measured from
- incident ray: A ray which meets the edge of a prism
- refracted ray: A ray which moves away from the edge of the prism having a change in velocity, and often a change in direction
- angle of incidence: The angle between the normal and the incident ray
- angle of refraction: Tha angle between the normal and the refracted ray
An experiment to see the effect of refraction on the direction of a ray can be seen using a semi-circular prism and a raybox. The light ray should be directed at the centre of the flat side of the prism. This is because any ray coming out of the curved side of the semi-circle must have come along a radius. The radius of any circle cuts the circumference at 90°. This means that the refracted ray exits the semi-circle along the normal.
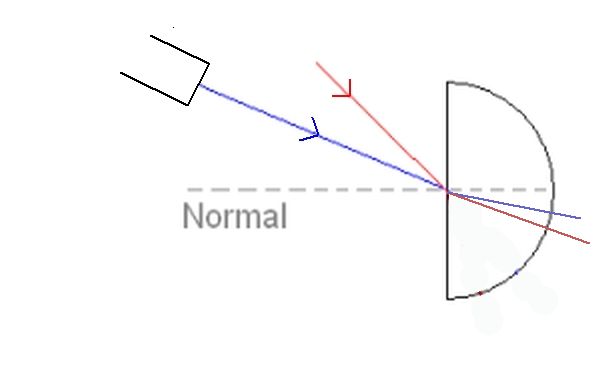
As can be seen in the diagram above the refracted rays have a greater angle than the incident rays. When an incident ray meets a more dense material the angle of refraction will always be greater than the angle of the incident ray.
To determine what happens when a ray moves from a more dense region to a less dense region can be shown by reversing the above experiment and shining the light into the curved face of the prism along the radius. The refracted ray will then exit from the centre of the flat side.
Another possibility is to use a rectangular prism and to measure two sets of angles. The first two angles are from the entry point of the ray to the prism. The second pair of angles are from the exit point of the ray from the other side of the prism. In the first pair of measurements the incident ray is from the air. In the second pair of measurements the incident ray is from the glass.
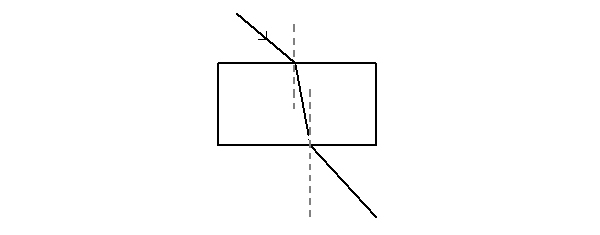
Looking at this diagram it can clearly be seen that as a ray goes from a less dense region to a more dense region that the angle of refraction is less than the angle of incidence. It can also be seen that a light ray going from a more dense medium to a less dense medium results in the angle of refraction being greater than the angle of incidence. In other words when light enters a more dense medium it bends towards the normal and when light enters a less dense medium it bends away from the normal.
Total Internal Reflection
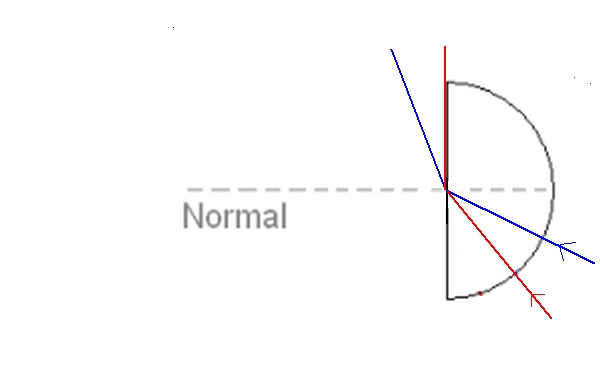
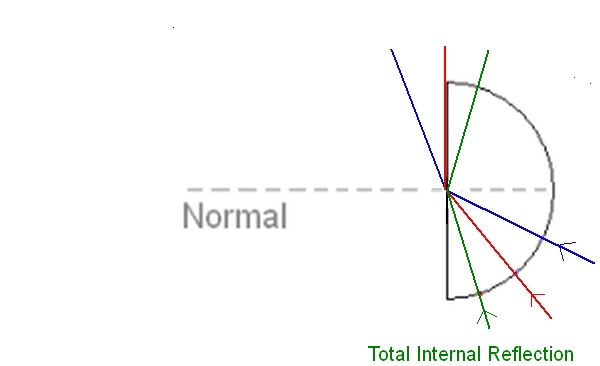
In the diagram below it can be seen that the angle of refraction for the red ray is 90° and that it runs along the flat face of the semi-circuar prism.

At any incident angles greater than this the light ray will be internally reflected. The angle at which light is refracted at 90° to the surface is called the critical angle. This term is defined by the refracted angle, NOT the total internal reflection. In the diagram below you can see the green ray has an incident angle greater than the critical angle and so it is totally internally reflected. For rays that are totally internally reflected, the laws of reflection apply. Total internal reflection can only occur when light is passing from a more dense medium to a less dense medium.
Total internal reflection is used in prismatic binocuars to increase the disance between the two lenses. It is used in cat's eyes - the refectors set into the middle of the road to reflect the light from car headlights back to the driver. It is also used in fibre optic lamps. One of the most important modern uses is in communications and the fibre optic cables used to send data signals across the globe.
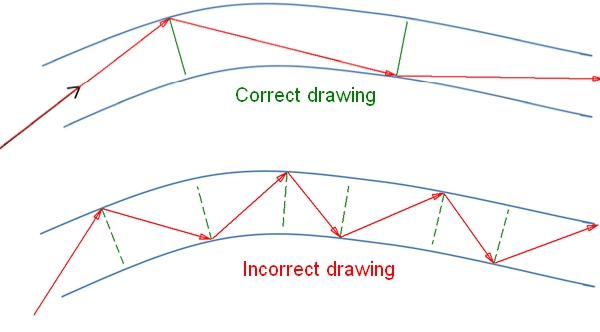
When a question from the SQA appears on TIR and fibre optic communication it is important to only draw very few reflections because the angle must be sifficiently great for TIR to occur. Folowing these rules will ensure a well drawn answer:
- All angles must be equal
- No more than 4 reflections should be shown in the fibre
- Include arrows to represent the light direction
- Use a pencil so if you can make a mistake you can easily start again
- Always use a ruler!