National 5 Physics

Wave Parameters and Behaviours - In progress

Waves are oscillations/vibrations that allow the transfer of energy without a net transfer of the medium carrying the wave.

All waves except electromagnetic waves require some medium to transmit them.

Types of Wave

Waves where the particles oscillate or vibrate at right angles to the direction of energy transfer are called transverse waves.

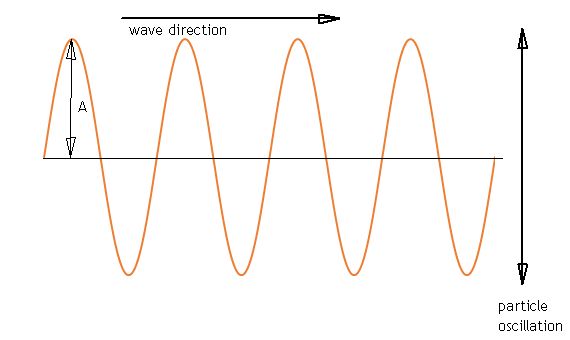
The arrow labelled A from the mid point of the wave to the top of the crest is called the amplitude of the wave.

Waves where the particles oscilllate or vibrate in the same direction as the energy transfer are called longitudinal waves.

Longitudinal	Transverse
Sound	Light
Ultrasound	Water
Seismic P waves	Seismic S waves

Match the wave term with its meaning

Wave Equations

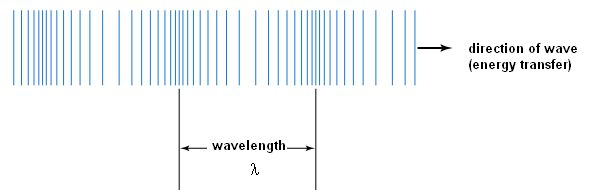
When looking at waves we need to think aboout how many waves pass a point in 1 second. This number is called the frequency of the wave. For example, if 4 waves pass a point in 1 second the frequency is said to be 4 Hz.
The equation to use in order to find out the frequency when you know the number of waves passing a point in a known amount of time is:

$$f=\frac{N}{t}$$

Where: f is the frequency
               N is the number of waves passing the point
               t is the time taken for the waves to pass

Example

25 waves pass through the harbour entrance in 10 seconds. What is the frequency of the waves?
N = 25; t = 25 s; f = ?
$$f=\frac{N}{t}$$ $$f=\frac{\mathrm{25}}{\mathrm{10}}$$ $$f=\mathrm{2.5\; Hz}$$

---

Interactive example 1 and solution

Attempt to solve the question yourself before clicking the solve button!

The number of waves passing a point is counted as . It takes minutes for this number of waves to pass. What is the frequency of these waves?

---

Wave Speed

What is the speed of a wave when the crest of a wave moves 40 m in 5 seconds

$$\mathrm{speed}=\frac{\mathrm{distance}}{\mathrm{time}}$$ $$v=\frac{d}{t}$$ $$v=\frac{\mathrm{40}}{5}$$ $$v={\mathrm{8\; m\; s}}^{\mathrm{-1}}$$

The equation linking speed of wave with the frequency and wavelength is:

$$v=\mathrm{f\lambda }$$

Where v = wave speed
               f is the frequency
               λ is the wavelength

Typical questions include:

A student, fishing from a pier, counts four waves passing the end of the pier in 20 seconds. The student estimates that the wavelength of the waves is 12 m.
Calculate the speed of the water waves.
This requires 2 steps to solve

Determine the frequency

$$f=\frac{N}{t}$$ $$f=\frac{4}{\mathrm{20}}$$ $$f=\mathrm{0.2\; Hz}$$

Determine the wave speed

$$v=\mathrm{f\lambda }$$ $$v=\mathrm{0.2}\times \mathrm{12}$$ $$v={\mathrm{2.4\; m\; s}}^{\mathrm{-1}}$$

What is the wavelength of a radio wave with a frequency of 1620 MHz?

This relies upon an understanding that radio waves are part of the electromagnetic spectrum. All waves from the electromagnetic spectrum in air have a speed of 3.0 × 10⁸ m s^-1. The prefix M infront of Hz indicates that we must mutiply the frequency by ×10⁶.

$$v=\mathrm{f\lambda }$$ $${\mathrm{3.0\; \times \; 10}}^8={\mathrm{1620\; \times \; 10}}^6\mathrm{\times \; \lambda }$$ $$\lambda =\mathrm{0.185\; m}$$

---

Determining wave velocity using distance and time with solution

Attempt to solve the question yourself before clicking the solve button!

A wave travels m in a time of seconds. What is the velocity of this wave?

---

Determining velocity using wavelength and frequency with solution

Attempt to solve the question yourself before clicking the solve button!

A wave with a wavelength of cm is found to have a freqeuncy of Hz. What is the velocity of this wave?

---

Determining frequency from wavelength and velocity with solution

Attempt to solve the question yourself before clicking the solve button!

A wave with a wavelength of mm has a velocity of m s^-1. What is the frequency of this wave?

---

Wave period

The period of a wave is the time it takes for a single wave to pass a point. This is the inverse of the frequency and is given in the relationship:

$$T=\frac{1}{f}$$

What is the frequency of a wave which has a period of 0.125 s?

$$T=\frac{1}{f}$$ $$\mathrm{0.125}=\frac{1}{f}$$ $$f=\mathrm{8\; Hz}$$

Diffraction

This is a property that all waves can demonstrate. When passing through a gap or meeting a barrier it is possible for waves to bend and spread out.

The amount of spreading out depends on the reationship between the wavelength of the wave and the size of the gap it is passing through. Where the gap size is similar to the wavelenght of the wave there is a lot of spreading out.

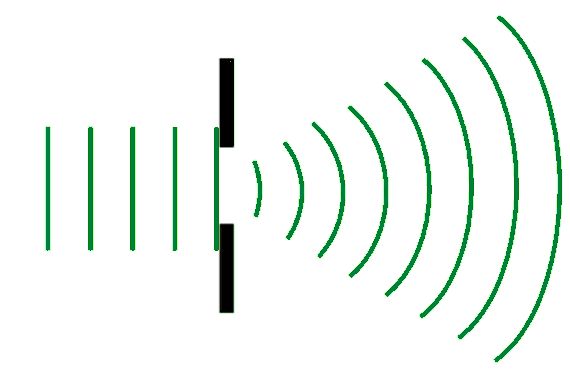
The diagram shows that waves are most effectively spread out when the gap size is similar to the wavelength. An everyday example of good diffraction is when you hear sound that has passed through a an open doorway. The waves get ver spread out and it is possible to hear the sound when standing well to the side of the doorway.

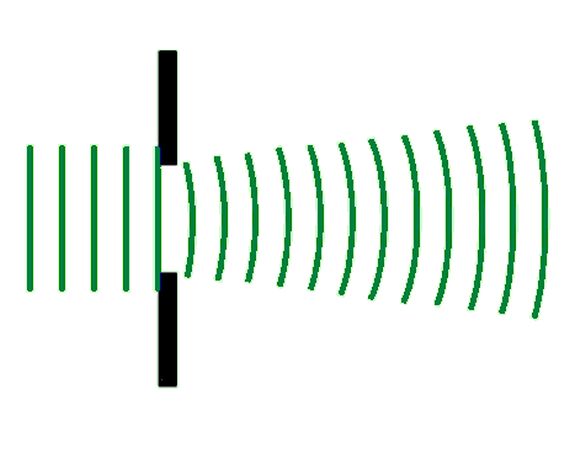
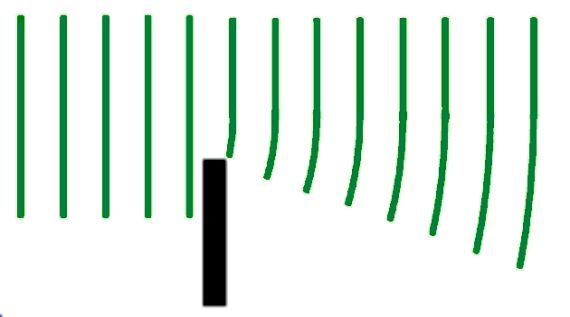
The diagram shows that the central part of the wave is unaffected by the gap in the barrier because this gap is much greater that the wavelength of the wave. There is still spreading out at the edges of the wave. In the national 5 examination if a question about this occurs it is very important to remember to keep the central part of the planar waves still planar.

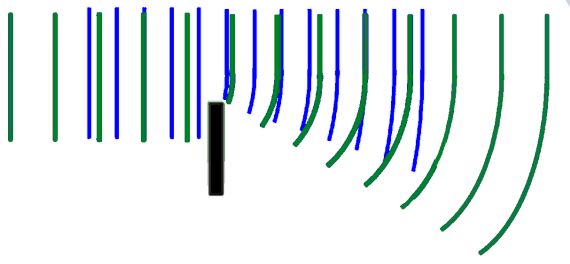
When waves diffract past an edge, the longer the wavelength the greater the amount of spreading out. This is very important when positioning TV and Radio transmitters because their long wavelengths mean that they can diffract past buildings and hills to provide signals in areas where the transmitter cannot be seen.

When we add these two diagrams together it is easy to see that the longer wavelength waves spread out more.

Wave Properties and behaviours can be found in the Physics with Answers Text book pages:

Blue Book - pp 64 - 77

Quick Quiz