Higher Physics

Forces on charged particles

Do you remember the Van der Graff generator where static electricity is generated? You may have seen pictures with a person's hair sticking up while they are attached to the Van der Graff generator.

We understand that charged particles with the same charge repel each other. Therefore the hair strands stick out from the head as they become more charged.

For the hair to move from sitting on the head, there must be some force to oppose the gravitational attraction for the hair. This force is due to the electric field that the charged particles on the surface of the hair produce. The greater the charge, the bigger the electric field.

Electric Fields

The simplest cases to consider are the electric fields for single isolated charges.

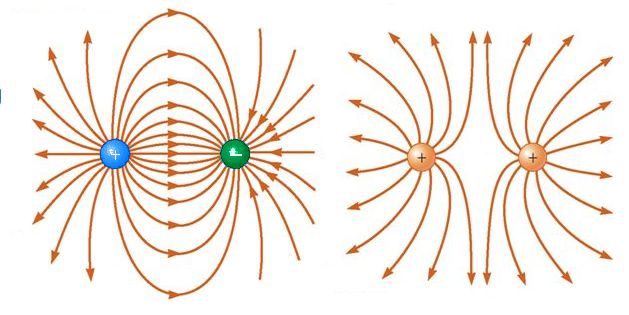
Below are diagrams showing the electric field for both a positive point charge and a negative point charge.

Remember an electric field is three dimensional - but we draw it as two dimensional for simplicity. Where the field is stronger the lines are drawn closer together.

Note that the field lines point away from the positive charge and point towards the negative charge. This is because the concept of current in physics is based on the movement of positive charge. We now know that the actual charges that move are the electrons which are negative. When dealing with current you must always apply the movement of positive charge in line with the direction of the current arrow, or component such as a diode or LED.

When we have two charge particles near each other the field lines can be seen in the diagram below. You need to be able to sketch these diagrams

When we have two parallel plates with opposite charges the following diagram shows the uniform nature of the field. This is illustraded because the field lines are the same distance apart from each other, and all pointing in the same direction. You may come across diagrams that show deviation at the edges of the plate, but this knowledge is not required at this level.

We know that, in conventional current terms, positive charges move towards negative charges and that opposite charges attract. We are also know that, in reality, current is due to the movement of electrons in wires, rather than positive charges. It is important to remember that convention is always about the movement of positive charge.

Charges will always move from a region of higher potential to one of lower potential. Therefore, when we apply an electric potential to a system there will always be movement of charge based on the direction of the field.

Consider a small positive charge in an electric field as shown in the diagram below:

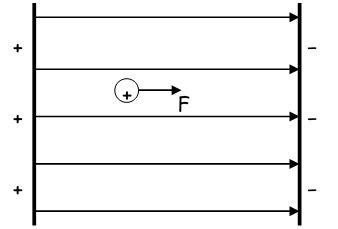
When the charge is released between the parallel plates a force is exerted on it. As it is a positive charge, the force acts in the direction of the electric field. It accelerates towards the negative plate.

The electric field is a uniform field. This is shown by the uniform spacing of the straight field lines. The unbalanced force is therefore constant, resulting in uniform acceleration.

This can be compared to the action of a gravitational force on an object. Uniform field, resulting in uniform accelertion.

Electrostatic Potential

Consider the small positive charge moved against the field as shown.

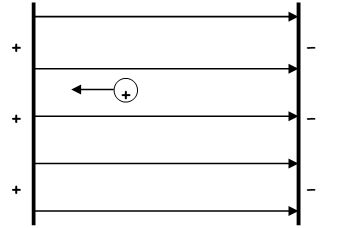
Work must be done to move the charge against the direction of force. When held in place, the small positive charge is an electrostatic potential store of energy.

We say that work done moving the charge against the field = the gain in electrical potential energy

Definition of potential difference and the volt

Potential difference (p.d.) is defined to be a measure of the work done in moving one coulomb of charge between two points in an electric field. Potential difference (p.d.) is often called voltage. This gives the definition of the volt.

There is a potential difference of 1 volt between two points if 1 joule of energy is required to move 1 coulomb of charge between the two points.

1V = 1 J C^-1

The relationship may be expressed:

$$E_w=\mathrm{QV}$$

where E_w is energy (work done) in joules (J), Q is the charge in coulombs (C) and V is the potential difference (p.d.) in volts (V).

In quantum physics the Joule is to large a quantity to use, and physicists use the electron volt as their energy unit of choice.

1 electron volt is defined as the energy one electron contains when it is moved through a 1 Volt potential difference.

$$E_w=\mathrm{QV}$$ $$E_w={\mathrm{1.6\; \times \; 10}}^{-19}\mathrm{(C)}x1\mathrm{(V)}$$ $$1\mathrm{eV}={\mathrm{1.6\; \times \; 10}}^{-19}J$$

If the small positive charge, above, is released there is a transfer of energy to kinetic energy, i.e. the charge moves. Again, using the conservation of energy means that:

$$E_w=E_k$$ $$\mathrm{QV}=\frac{1}{2}m{v}^2$$

An electric charge in an electric field will experience a force and will be accelerated by this force. The work done on the charged particle is

$$W=\mathrm{QV}$$

With this equation it is possible to calculate the energy transferred to the charged particle by the electric field if we know the potential difference through which the charged particle is accelerated. Let us consider a uniform electric field between two plates.

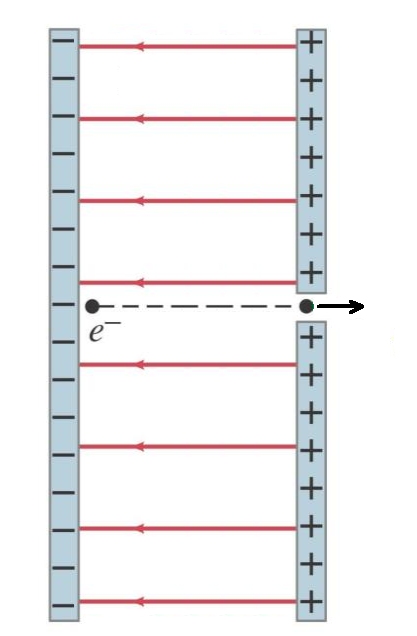
The electron starts from rest at the negative plate and is accelerated by a potential difference between the two plates of 1.00 kV, through the hole in the positive plate. As the electron reaches the hole in the positive plate calculate how much work has been done by the electric field on the electron. Determine the speed of the electron at this point.

We know that the work done is equivalent to

$$E_w=\mathrm{QV}$$

Knowing the charge on an electron is 1.6 × 10^-10 C and the potential difference is 1000 V, we can calculate the work done

$$E_w={\mathrm{1.6\; \times \; 10}}^{\mathrm{-19}}\mathrm{ \times \; 1000}$$ $$E_w={\mathrm{1.6\; \times \; 10}}^{\mathrm{-16}}J$$

Knowing the work done E_w = 1.6 × 10^-16 J we can use conservation of energy to calculate the speed from the kinetic energy gained by the electron.

$${\mathrm{1.6\; \times \; 10}}^{\mathrm{-16}}=\frac{1}{2}{\mathrm{mv}}^2$$ $${\mathrm{1.6\; \times \; 10}}^{\mathrm{-16}}=\frac{1}{2}\mathrm{ \times }{\mathrm{9.11\; \times \; 10}}^{\mathrm{-31}}{\mathrm{\times \; v}}^{\mathrm{2<!--,i-->}}$$ $$v={\mathrm{1.9\; \times \; 10}}^7{\mathrm{m\; s}}^{\mathrm{-1}}$$

---

Work done, speed and voltage

Attempt to solve the question yourself before clicking the solve button!

A proton of mass 1.673 × 10^-27 kg was initially stationary and then experienced an electric field that does × 10^-18 J of work on it.
(a) Calculate the speed of the proton assuming all the work is converted to kinetic energy.
(b) Determine the potential difference between the two plates that provided this energy to accelerate the proton.

---

Charges moving in Magnetic Fields

When current flows through a wire a magnetic field is produced around the wire. Simple rules can be used to determine the direction of force on a charged particle in a magnetic field.

Movement of a positive charge in a magnetic field

One way the motion of a charge particle can be determined is the use of Fleming's Left Hand Rule.

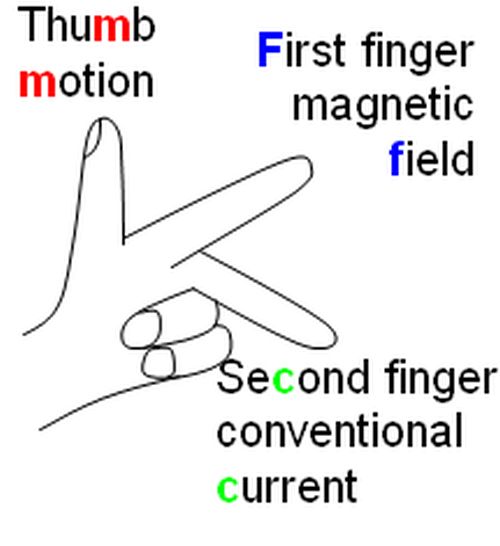
To help remember the use of the left hand as a guide to motion of charged particles in a magnetic field it may help to think of the alphabet, where abcde...LM...wqyz reminds you that Left is Motion

Example 1

How will an electron move when it passes vertically through a crossed magnetic field, where the uniform magnetic field has the north pole on the left and the south pole to the right?

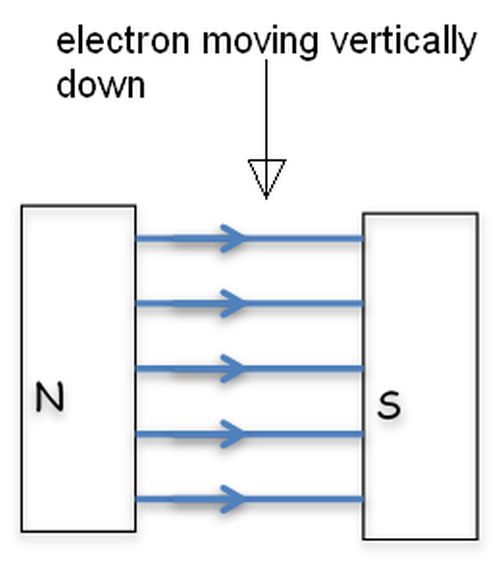
In conventional current terms the second finger points up, as conventional current is opposite to the movement of electrons. The First finger points over to the left. The result is that the thumb points into the page. Therefore the electron is accelerated into the page and travels in a curve into the page.

Example 2

An electron is accelerated from rest by a potential difference of 2 kV. How fast is it moving as it exits the accelerating field?

$$E_w=E_k$$ $$\mathrm{QV}=\frac{1}{2}m{v}^2$$ $${\mathrm{1.6\; \times \; 10}}^{-19}\times 2000=\frac{1}{2}\times {\mathrm{9.11\; \times \; 10}}^{-31}\times v^2$$ $$v={\mathrm{2.65\; \times \; 10}}^7{\mathrm{ms}}^{-1}$$

---

Work done, speed and voltage

Attempt to solve the question yourself before clicking the solve button!

An electron was initially at rest when it was accelerated by an electric field that resulted in a final velocity of × 10⁶ m s^-1.
(a) Calculate increase in kinetic energy of the electron.
(b) Determine the potential difference between the two plates that provided this energy to accelerate the electron.

---