Higher Physics

Inverse Square Law

Power of the Sun

The Sun is radiating energy in all directions and here on Earth we can work out how much energy is received on the surface per square metre. Professor Brian Cox shows in the video how this was worked out by John Herschel in the early 1800's.

Brian Cox on the BBC - Power of the Sun

When looking at the power output from a point source of light (simple filament lamps provide a good approximation) there is a relationship to power of the source and the amount of light recieved per unit area. This is given by the following equation:

$$I=\frac{P}{A}$$

• I = irradiance (W m^-2)
• P = power (W)
• A = area (m²)

From the relationship we can see that the definition of irradiance is the power per unit area of light incident on a surface. The units are therefore Watts per metre squared (W m^-2).

Example 1

The power from a lamp is measured as 0.25 W across an area of 100 cm². Calculate the irradiance of the lamp.

• P = 0.25 W
• A = 100 cm² = 0.01 m²

$$I=\frac{P}{A}$$ $$I=\frac{\mathrm{0.25}}{\mathrm{0.01}}$$

I = 25 W m²

The inverse square law

A simple experiment to carry out with a lamp, a light meter and a ruler is to measure the effect of distance on the irradiance from the lamp as it is moved away from the meter. A diagram of the experiment is given below.

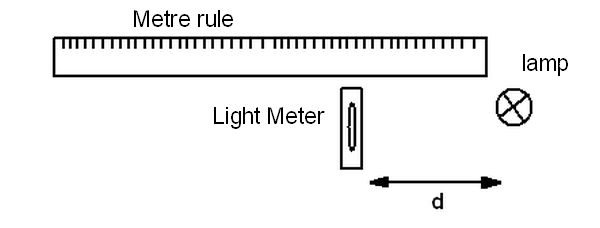
The surface of the desk should be darkened to avoid reflection and the room darkened, with no other sources of light to determine the relationship.

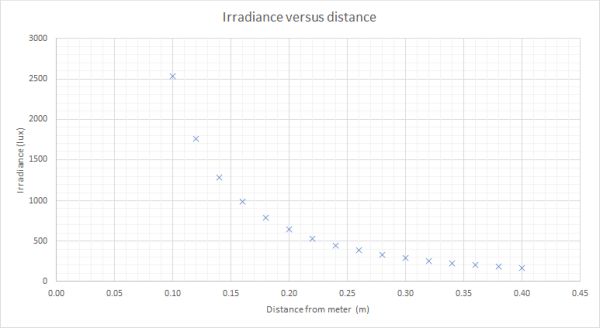
A table of results is given below

Distance to meter (m)	Irradiance (lux)
0.10	2532
0.12	1753
0.14	1286
0.16	992
0.18	784
0.20	646
0.22	531
0.24	448
0.26	383
0.28	331
0.30	287
0.32	253
0.34	225
0.36	202
0.38	187
0.40	167

On plotting these results we get a curve showing an inverse relationship between irradiance and distance

When the irradiance is plotted against 1/d² the graph shows direct proportionality. Therefore irradiance is inversely proportional to the square of the distance from a point source. The graph of the above data is shown below:

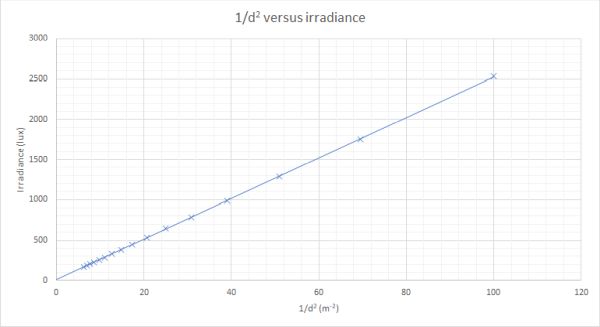
This graph allows us to develop the other two relationships required in the course.

$$I=\frac{k}{d^2}$$

Where k is the gradient of the straight line (or the constant of proportionality). This also leads on to being able to compare two results directly using:

$$I_1{d}_1^2=I_2{d}_2^2$$

Questions

Example 2

The Irradiance of light from a point source is 10 Wm^-2 at a distance of 5 m from the source. Calculate the Irradianceof the light at a distance of 25 mfrom the source.

• I₁ = 10 Wm^-2
• d₁ = 5 m
• I₂ = ?
• d₂ = 25 m

$$I_1{d}_1^2=I_2{d}_2^2$$ $${\mathrm{10\; \times \; 5}}^2=I_2{\mathrm{\times \; 25}}^2$$

I₂ = 0.40 Wm^-2

Example 3

The light irradiance of a 40 W lamp is measured by a pupil with a light level meter to be 1.6 Wm^-2 at a distance 1.5 m from the lamp.
Calculate the light irradiance at a point 0.75 m from the lamp

• I₁ = 1.6 Wm^-2
• d₁ = 1.5 m
• I₂ = ?
• d₂ = 0.75 m

We can see that the distance has halved so 1/2² = 1/4, therefore the light has 4 times the power

I₂ = 6.4 Wm^-2

Watch out for simple ratios like this it can speed up the calculation.