Higher Physics

Spectra

Introduction

In the late 1800s and early 1900s our knowledge of the atom increased from the plum pudding model to one where there was a tiny nucleus. Rutherford's alpha particles fired at gold foil showed that all of the mass of the atom was concentrated in a tiny volume at least 4 orders of magnitude smaller than the size of atoms. It was also shown that all of the positive charge was concentrated in this centre part. This led a a problem for physicists at the time. How could atoms exist, because the positive charge of the nucleus would electrostatically attract the negatively charge elecrtrons. Why did the electrons not just collapse into the nucleus radiating out energy as they crashed in to the nucleus. A new way of thinking had to be developed, based on experimental results and consistent with the laws of physics.

Quantum theory

A simple experiment with hydrogen provided key evidence for a new type of thinking. When hydrogen atoms are excited they produce a coloured light. The colour is a pale purple. This light can be refracted through a prism to look at its spectrum. Oddly the spectrum was not a continuous spectrum, like the rainbow formed when white light passes through a prism.

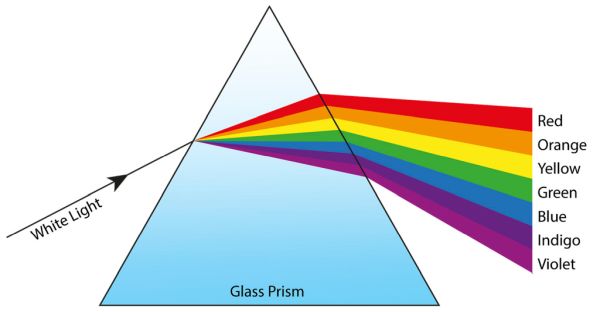
Instead the spectrum was made of discrete lines as can be seen below:

Why were there only specific frequencies of light being produced by excited hydrogen atoms?

The concept of quantisation was proposed by Max Planck and in 1900 he developed the following equation E = hf. This was a radical departure from classical physics because the energy of a wave was no longer the amplitude. According to Planck the energy of light waves is defined by the frequency of the wave. When this is applied to the Balmer lines it appears that the electrons in hydrogen are in quantised energy levels. This new idea allowed scientists to propose that the quantisation of energy level results in the electrons being unable to spiral into the nucleus. Electrons can only exist in specific energy levels which they can move between, but they cannot exist at any other inbetween energy levels.

Bohr Model

In 1913 Bohr propsed a quantised shell model for the electrons in an atom. The orbits are sperical and numbered from the closest to the nucleus, with number 1, out in integer values. Electrons were able to move between these layers by absorbing energy when moving up the energy levels way from the nucleus and giving out energy when moving down. The energy absorbed or emitted is in the form of light.

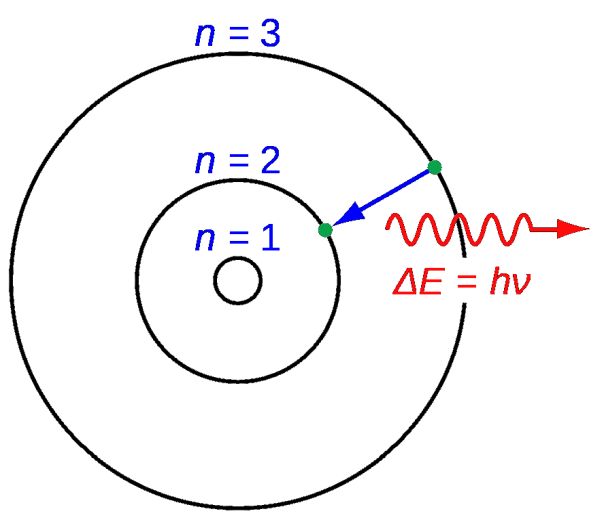
Let us look at electron structures in hydrogen. Remember this is an atom with only one electron. When the electron is in the lowest possible energy state we say that the electron configuration is in the ground state.

When the electron is moved up to the next highest energy level we say that it is in the first excited state. The next level up is the second excited state, and so on.

When the electrons are moved up in energy levels a fixed quantity of energy is required by the electron based on the energy difference of the two initial and final energy levels. When the electrons return to lower energy levels then specific frequencies of light are given out. This is shown in the image below.

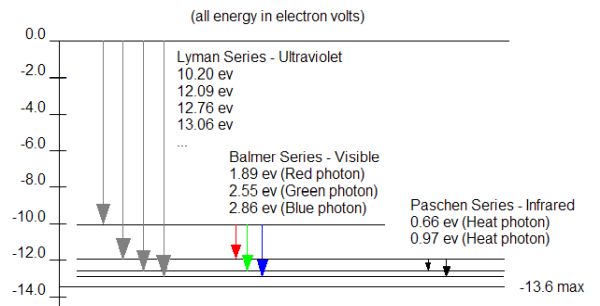
Zero Energy Level

You may have noticed in the diagram above that the energy levels start with 0 at the top and become increasingly negative as the electron gets closer to the nucleus. Physicists define the zero potential energy as the poiint at which the electron is at an infinite distance from the nucleus. This means that we have to do work on the electron to move it to a higher energy level. In the case of hydrogen this will require 13.6 eV of energy to remove the electron from the atom. This is called the ionisation energy. When looking at the emission spectra of hydrogen it is possible to determine this level by looking at the Lyman (U.V.) spectrum of hydrogen. Where the lines converge, at the upper limit we have the energy required to ionise hydrogen.

Fraunhofer Lines

A German scientist, Joseph von Fraunhofer, observed that the spectrum of sunlight had dark lines in it, where specific frequencies of light appeared to be missing. We now understand that light from the sun passes through elements in its outer atmosphere. The elements present in the outer atmosphere are responsible for the missing lines due to their electrons absorbing energy to be promoted. Each element has its own specific energy levels and so it possible to determine which elements are present in the outer atmosphere of the sun.

Calculations

Example 1 (a)

An electron descends from the third shell to the second shell in an atom of hydrogen. What is the frequency of the light emitted?

$$E_2-E_1=\mathrm{hf}$$ $${\mathrm{-2.42\; \times \; 10}}^{\mathrm{-19}}-{\mathrm{(-5.42\; \times \; 10}}^{\mathrm{-19}})=\mathrm{hf}$$

f = 4.52 × 10¹⁴ Hz

Example 1 (b)

What is the colour of light with a frequency of 4.52 × 10¹⁴ Hz?
c = fλ
3 × 10⁸ = 4.52 × 10¹⁴ × λ
λ = 663 nm - which is red in colour.

Example 2

Light of wavelength 490 nm is measured in the absorption spectrum of hydrogen. What is the difference in the energy level of the two energy levels?

Remember that f = c/λ

$$E=\mathrm{hf}$$ $$E=h\frac{c}{\lambda }$$ $$E=h\frac{{\mathrm{3\; \times \; 10}}^8}{{\mathrm{480\; \times }}^{\mathrm{-9}}}$$

E = 4.06 × 10^-19 J

---

Energy and light

Attempt to solve the question yourself before clicking the solve button!

The energy difference between two quantum levels in an isolated atom were × 10^-19 J.
(a) Calculate the frequency of light associated with this energy change.
(b) Determine the wavelength of this light.

---

Energy and light

Attempt to solve the question yourself before clicking the solve button!

Light of a visible wavelength of nm was detected in the line spectra of an element.
Calculate the energy change between the two energy levels which produced this wavelength of light.

---