Higher Physics

Interference

A great app for looking at wave behaviour is the ripple tank app at falstad.com. The link is here: Ripple Tank

One of the strongest evidences for wave behaviour is the abilit of waves to interfere with each other. This is most remarkable when two waves travelling in opposite directions apeat to cancel each other out before coninuing on their way.

Consider a slinky where both ends are used to produce a single wave in opposite direcations on opposite sides of the slinky. See diagram one:

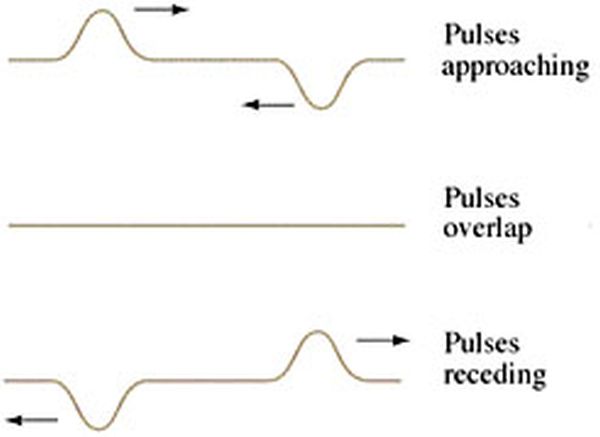
Notice the middle line, where the pulses appear to have momentarily disappeared, but then the waves contine on, transferring the energy they contain.

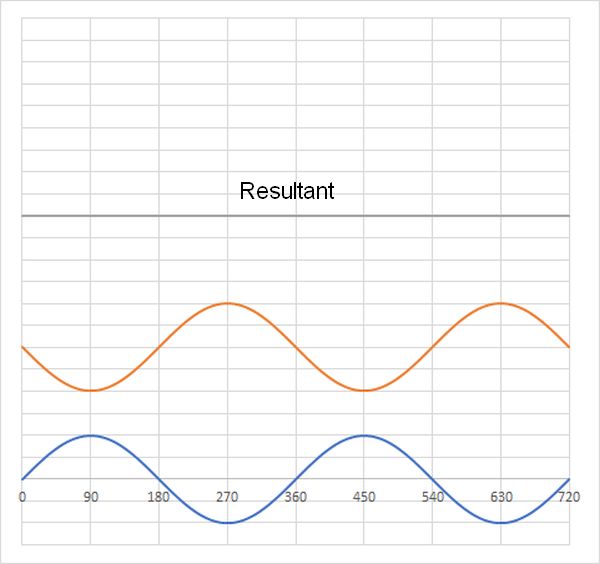
Consider the case when both pulses are on the same side of the slinky, but from opposite ends. See the result in the diagram below:

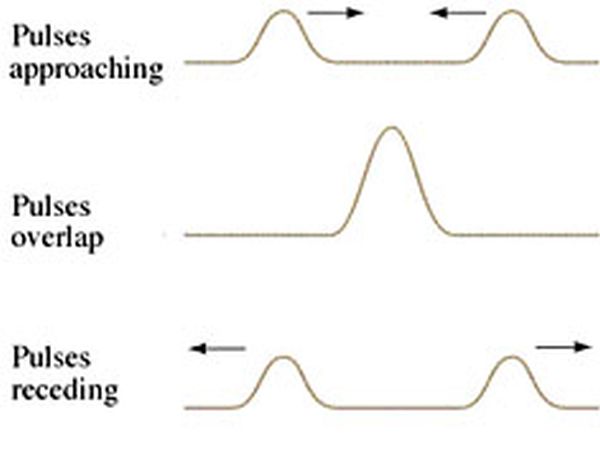
Note that at any point in time the two waves can be added to produce a combined wave. This addition of waves is called superposition of waves. This concept is important when we consider adding waves together which are produced by two sources.

Coherence and Phase

In this course we will predominantly consider waves that are equal in amplitude, with the same frequency and wavelength. We will consider phase difference, which refers to the horizontal distance between two similar parts of each wave. Consider the diagram below where you can see the 90° phase difference between a sine wave and a cosine wave.

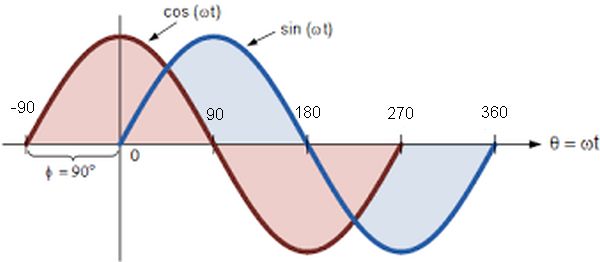
When two waves have a constant phase difference we say that they are coherent. The University of Salford Manchester has a great app for looking at phase relationships of coherent waves.

Phase Difference

There are two extremes when considering the pahse of two waves. The first one is when they are in phase, and that results in the crests adding to give a result with twice the amplitude.

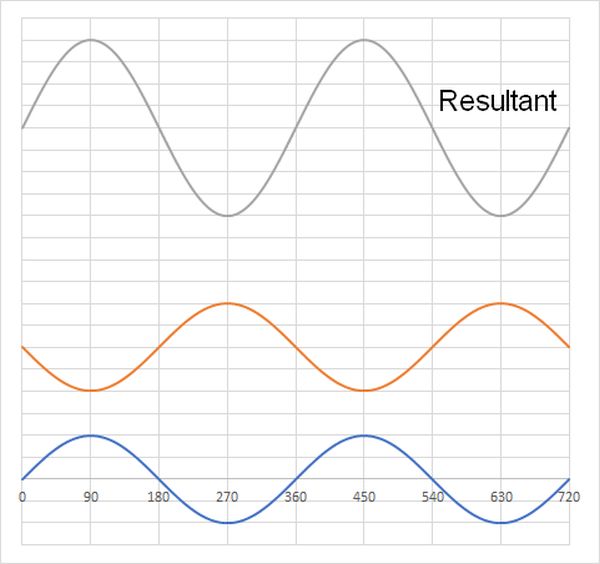
The other extreme is when the two waves have a phase angle of 180°. We say that the waves are out of phase and when they add together they cancel each other out.

Interference

Below is an image formed when two coherent sources produce waves of the same amplitude side by side

You can clearly see that there are regions where the waves have added together to give maxima, and regions where they have added to cancel each other out.

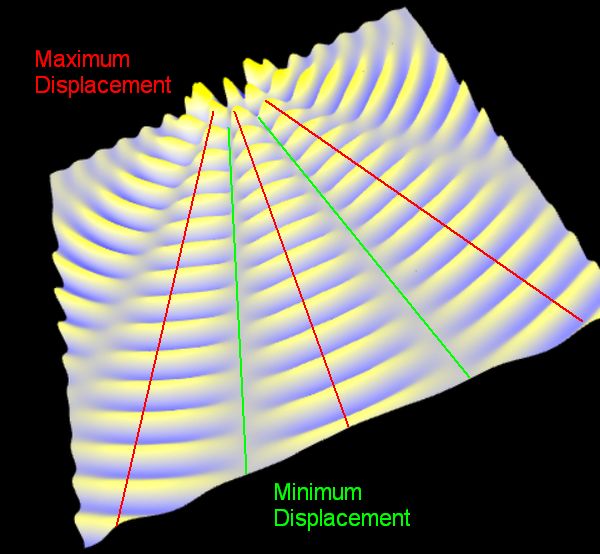
The maxima are called regions of constructive interference.

The minima are called regions of destructive interference.

Interference is a property only associated with waves.

Light is a wave

In order to show that light is a wave we need to carry out an experiment that shows wave tyoe behaviour. The classic experiment for this is to use a double slit, with a single source of light. The experiment is named after Thomas Young, who carried out a similar experiment using sunlight in 1801.

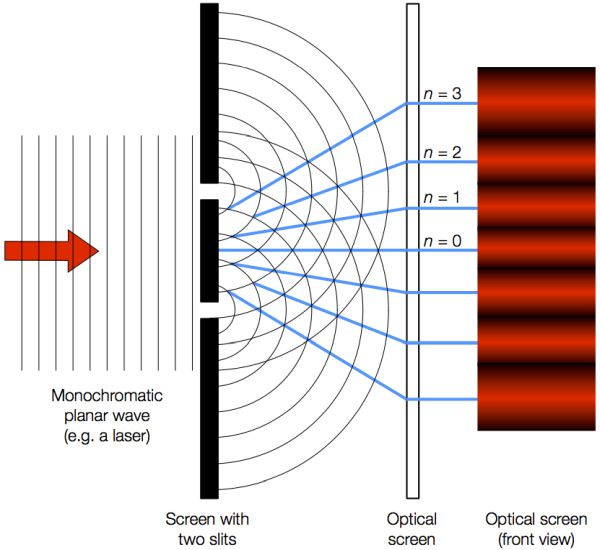
Notice that the pattern is symmetrical about the central maximum. Let us look in closer detail at the reason for the pattern that has been formed.

First we must know the conditions for constructive and destructive interference. When two oherent waves are a whole integer number of wavelengths apart they will constructively interfere to make maxima. When two coherent waves are an odd number of half wavelengths apart they will cancel each other out and destructively interfere. This can be seen in the images above.

Let us consider the path length of the waves. Look at the diagram below. Using a bit of geometry we can determine the difference in path length between the two waves based on the width of the slits, the distance to the screen and the angle from the normal to the ray

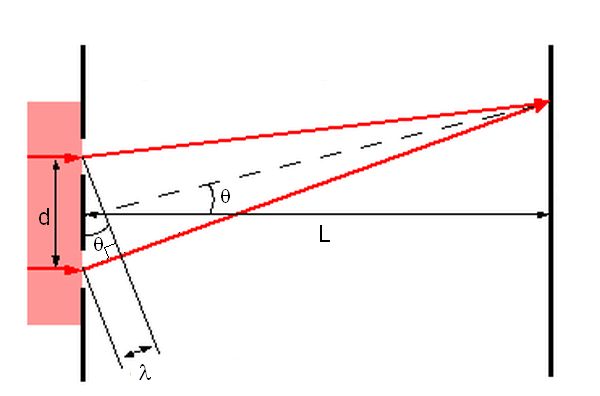
The distance of added path length in the diagram is λ. From the right angle triangle the relationship is

$$sin\theta =\frac{\lambda }{d}$$

Providing the distance λ is a whole number of wavelengths the equation can be rearranged to include the integer 'm'.

$$dsin\theta =\mathrm{m\lambda }$$

This is the condition for constructive interference. Therefore providing we know the wavelength of the light being used we can determine the angle at which a maximum or a minimum will form. All we need to remember is that with a path difference = mλ or = m (1/2 + λ) where m = 0,1,2... we will get constructive or destructive interference respectively.

Diffraction Gratings

Young's double slit experiment results in maxima that are quite spread out. When we increase the number of slits for the light to pass through the resolution of the position of the maxima improves.

The condition for maximum intensity is the same as that for a double slit. However, angular separation of the maxima is generally much greater because the slit spacing is so small for a diffraction grating.

Calculations

Example 1

Here is a past paper Multiple Choice Question

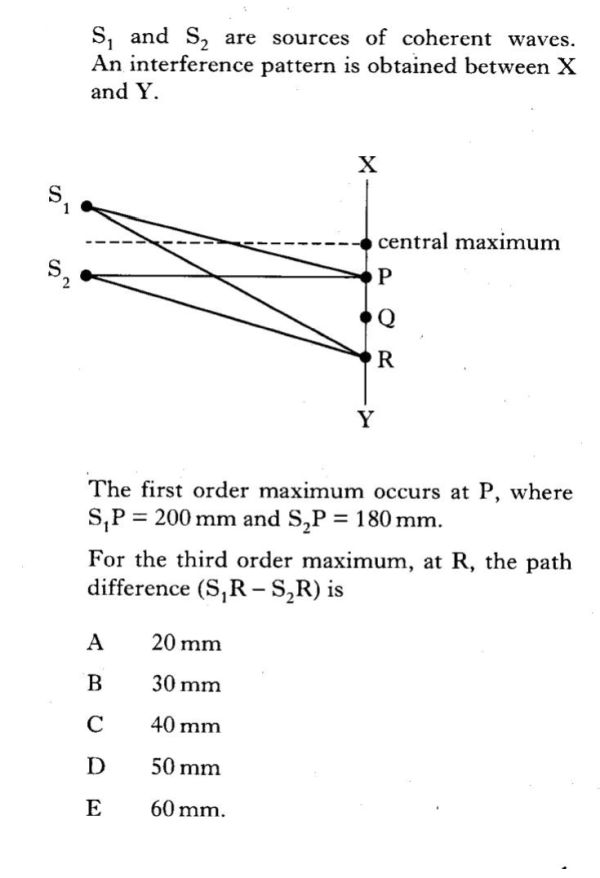
• Path length S₁P = 200 mm
• Path length S₂P = 180 mm

We can see from the question that the difference in the path length of the two rays is 200 mm - 180 mm = 20 mm. This is the the path length difference for the first order, or 1 × λ. The questions asks for the path length difference when m = 3.
3 × 20 mm = 60 mm. Therefore answer E is the correct answer.

Example 2

In this multiple choice question the grating slit width is to be calculated, the value of d.

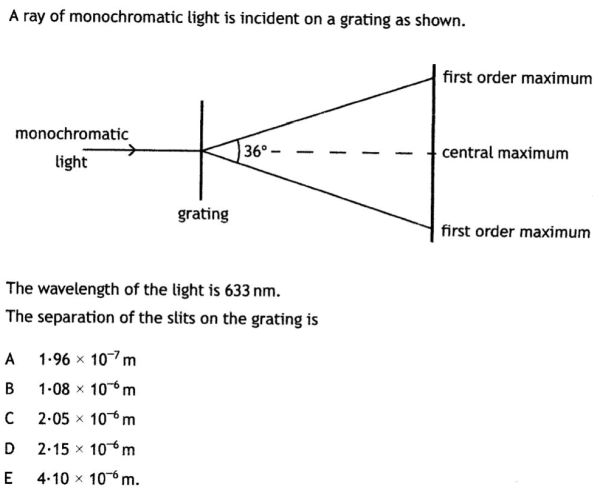
Notice that in the question there is an angle given, but it is twice the value of θ, which is a common device used by the SQA to check to see if candidates understand that the value of θ is from the normal, not the angle between the two maxima.

• θ = 36/2 = 18°
• λ = 633 × 10^-9
• m = 1

$$dsin\theta =\mathrm{m\lambda }$$ $$dsin\; 18°={\mathrm{1\; \times \; 633\; \times \; 10}}^{\mathrm{-9}}$$

d = 2.05 × 10^-6 m. Therefore answer C is the correct answer

Example 3

A student makes the following statements about waves from coherent sources.

• I - Waves from coherent sources have the same velocity.
• II - Waves from coherent sources have the same wavelength.
• III - Waves from coherent sources have a constant phase relationship

Which of these statements is/are are correct?

• A I only
• B II only
• C I and II only
• D I and III only
• E I, II and III

The three statements are all correct and so answer E is the correct answer.

Example 4

A manufacturer claims that a grating consists of 3.00 × 10⁵ lines per metre and is accurate to &plusminus; 2.0%. A technician decides to test this claim. She directs laser light of waveleingth 633 nm onto the grating.

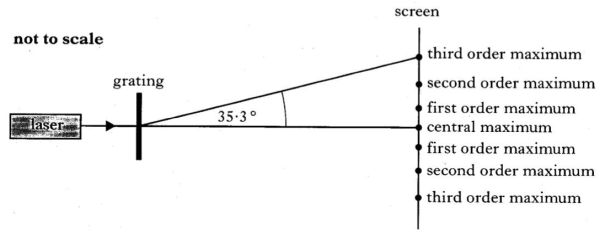
She measures the angle between the central maximum and the thrid order maximum to be 35.3°.
(a) Calculate the value she obtains for the slit separation for this grating.

• m = 3
• θ = 35.3°
• λ = 633 × 10^-9 m
• d = ?

$$dsin\theta =\mathrm{m\lambda }$$ $$dsin\; 35.3°={\mathrm{3\; \times \; 633\; \times \; 10}}^{\mathrm{-9}}$$

d = 3.29 × 10^-6 m

(b) What value does she determine for the number of lines per metre for this grating?

• d = 1 m
• grating spacing = 3.29 × 10^-6 m

Number of lines per metre = 1/3.29 × 10^-6 m

3.04 × 10⁵ lines per metre

(c) Does the technician's value for the number of lines per metre agree with the manufacturer's claim of 3.00 × 10⁵ lines per metre &plusminus; 2.0 %?
You must justify your answer by calcualtion

The limit of the uncertainty is 2.0%. therefore calculating 3.00 × 10⁵ + 2.0% will allow us to see if the claim is correct.

the value of 2.0% = 3.00 × 10⁵ × 2.0/100 = 0.06 × 10⁵
This is greater than the 0.04 × 10⁵ greater value found by the technician. This means that the claim is correct.