Higher Physics

Refraction of light

Speed of light

Light travels at its fastest speed in a vacuum. The speed of light is given as 3.00 × 10⁸ m/s. Scientists have determined that the actual speed of light in a vacuum is 299 792 458 m/s, which as you can see rounds to 300 000 000 m/s or 3.00 x 10⁸ m/s. We will use this rounded figure throughout the remainder of this course.

Refractive index

When the speed of light is measured in any material other than a vacuum it will be travelling slower than 3.00 x 10⁸ ms^-1. In air the speed is slowed to 299,704,645 ms^-1. This rounds to 3.00 x 10⁸ ms^-1. For most purposes we can therefore regard the speed of light in air as the same as the speed of light in a vacuum.

All absolute refractive indices are measured relative to the speed of light in a vacuum. For practical purposes, since the speed of light is the virtually the same in air, we use values of refractive index based upon the speed of light in air. You should remember this subtle distinction.

In National 5 you saw that refraction resulted in light changing direction when it moved from one medium to another with different optical densities when the incident ray is not aligned with the normal.

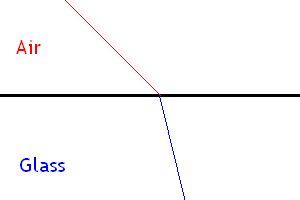
The key fact to remember about refraction is not the change of direction. The key fact is the change of speed. Remember light always slows down when it enters a more optically dense material. The ratio of the speed in the material to the seed of light in a vacuum is called the refractive index and is expressed in the following equation

$$\mathrm{n }=\frac{v_1}{v_2}$$

Where n is the refractive index
v₁ is the speed of light in a vacuum and
v₂ is the speed of light in the medium.

Since v₁ is the fastest speed of light, the value of n will always be greater than 1, because v₂ is always smaller than v₁

One thing that always remains the same is the frequency of the light. The speed and the wavelength will change, but the frequency will always remain unchanged.

Example Calculation

Calculate the speed of light in crown glass which has a refractive index of 1.52 (no units).

$$\mathrm{n }=\frac{v_1}{v_2}$$ $$\mathrm{1.52}=\frac{{\mathrm{3.00\; \times \; 10}}^8}{v_2}$$ $$v_2=\frac{{\mathrm{3.00\; \times \; 10}}^8}{\mathrm{1.52}}$$ $$v_2={\mathrm{1.97\; \times \; 10}}^8{\mathrm{m\; s}}^{\mathrm{-1}}$$

---

Interactive example and solution

Attempt to solve the question yourself before clicking the solve button!

A beam of light travels at a speed of m s^-1 through a material. Determine the refractive index of the material that it is travelling in.
(Nubers in the box will be displyed in the computer form where e+8 represents x 10⁸)

---

Experimental Determination of Refractive Index

You should know this experiment for the exam

Experimentally it has been determined that the ratio of the speed of light in different materials can also be determined by looking at the change in angle of incident and refracted rays. This is most easily done using a semi-circular prism. The reasoning for using the prism is that any ray directed towards the centre of the flat side prism will be perpendicular to the surface on the curved side of the prism. It is known that any ray travelling along a normal (a line perpendiular to the surface) does not change direction on passing from one medium to another.

This means that a refracted ray travelling along a radius will continue in a straight line to the protractor that is printed on the experiment sheet with the semi-circular prism. The angle of incidence and the angle of refraction can then be determined.

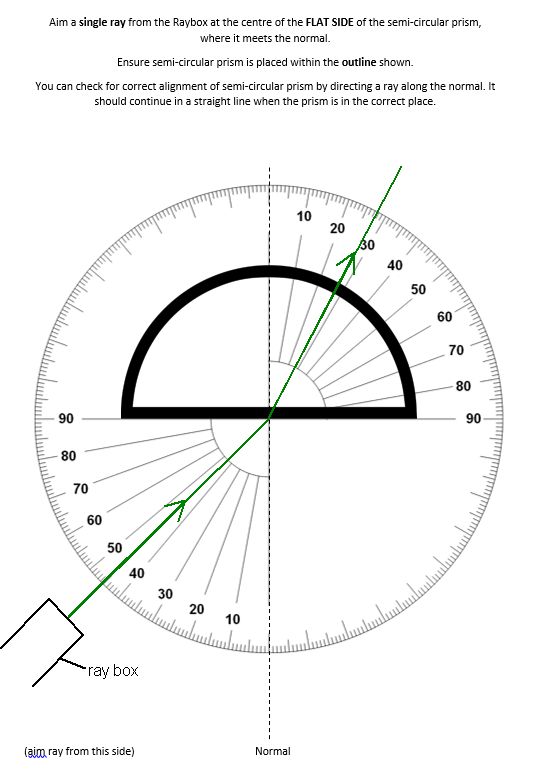
We can use the relationship below to determine the refractive index of the material.

$$n=\frac{{\mathrm{sin\; \theta }}_1}{{\mathrm{sin\; \theta }}_2}$$

Rearanging this equation gives us

$${\mathrm{sin\; \theta }}_1=n{\mathrm{sin\; \theta }}_2$$

Plotting a graph with sin θ₁ against sin θ₂ where θ₁ refers to the incident angle and θ₂ refers to the refracted angle will result in a straight line through the origin with a gradient equivalent to the refractive index of the material.

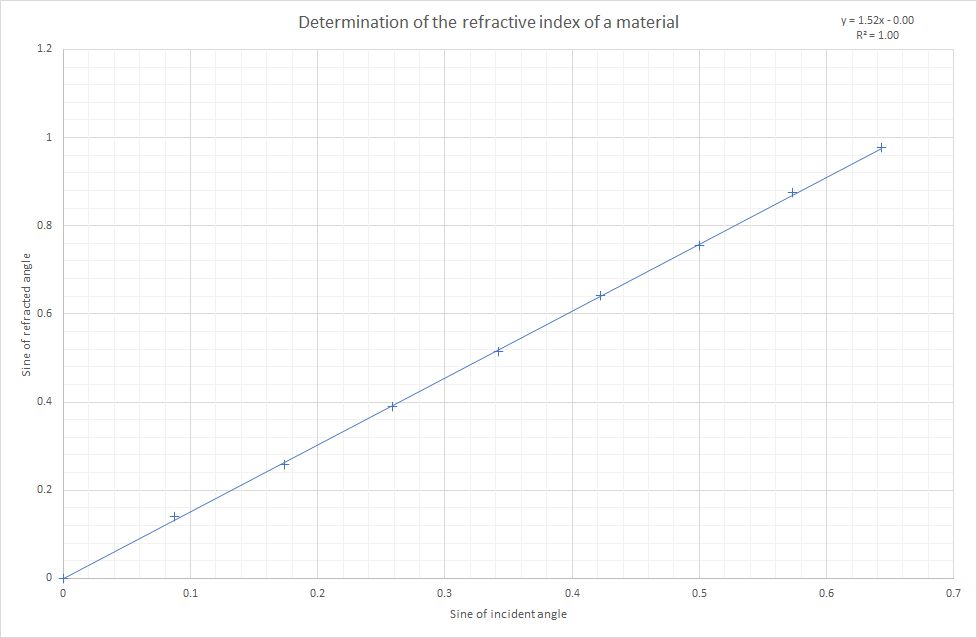
As can be seen in the graph above the gradient of the line is 1.52 and this is therefore the refractive index of the material for the specific colour of light used.

Experimental Determination the Critical Angle

When a ray of light is in a more dense material and being refracted into a less dense material there will be a value for the incident ray in the more dense material producing a refracted ray in the less dense material that is at 90° to the normal. This angle is known as the critical angle.

An experiment can be carried out to find the critical angle using a semi-circular prism where the incident ray is directed in along a radius of the curved side of the prism to the centre of the flat side. The refracted ray in air will be refracted away from the normal. The incident ray can be increased to the point where the refracted ray is at 90° to the normal. This is the critical angle.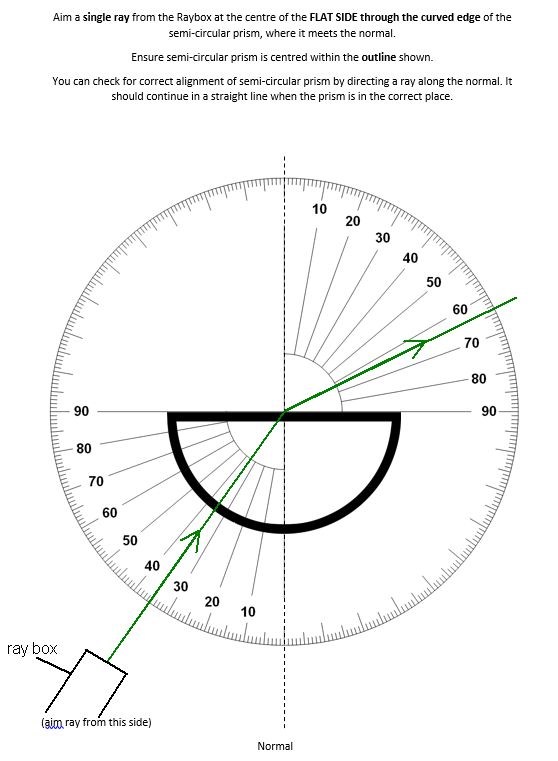

The critical angle can also be determined directly from the refractive index of the material. The following equations shows the relationship between critical angle and refractive index:

$${\mathrm{sin\; \theta }}_c=\frac{1}{n}$$

Condsider diamond with a refracive index of 2.42. Calculate the critical angle for diamond. $${\mathrm{sin\; \theta }}_c=\frac{1}{n}$$

Sibstituting in the value for the refractive index gives us:

$${\mathrm{sin\; \theta }}_c=\frac{1}{\mathrm{2.42}}$$

Evaluating to detrmine the value for θ_c gives us a value of 24.4° This very small critical angle is one of the reason that diamonds are so sparkly.

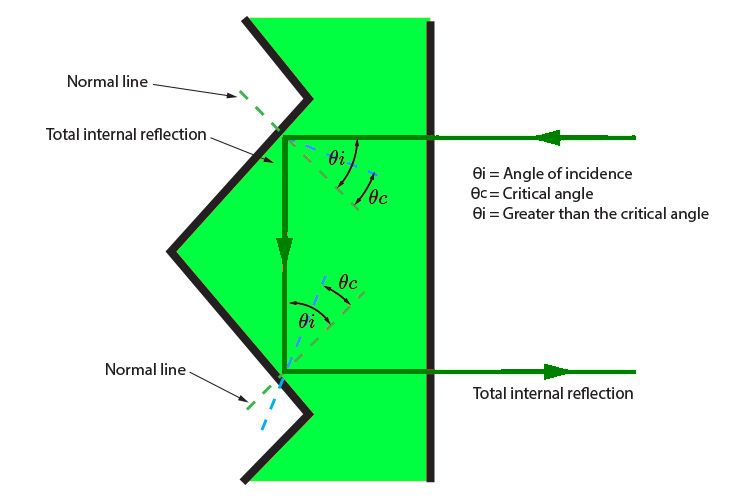
Remember that critical angle can only be determined in situations where the light is already in the more dense material and meeting at a boundary with a less dense material. At any angle of incidence greater than the critical angle in the more dense material the light will totally internally reflect. The angle of incidence will be equivalent to the angle of reflection at this surface. The property of total internal reflection is used in cat's eyes on our roads as well as in communication using fibre optics.

Terms associated with refraction

Refraction Relationships

In the syllabus the following relationships are equated in the relationship sheet.

$$\frac{{\mathrm{sin\; \theta }}_1}{{\mathrm{sin\; \theta }}_2}=\frac{{\lambda }_1}{{\lambda }_2}=\frac{v_1}{v_2}$$

It is left to students to appreciate that the following is also true:

$$n=\frac{{\mathrm{sin\; \theta }}_1}{{\mathrm{sin\; \theta }}_2}=\frac{{\lambda }_1}{{\lambda }_2}=\frac{v_1}{v_2}$$

Notice that the refractive index of a material can be determined using sines, wavelengths or speeds of light. In all cases the value of sinθ₁, λ₁ and v₁ are values for light in a vacuum. Remember that we substitute in the values of light in air because of the closeness in the two values.

Example Calculation

Calculate the wavelength of green light (509 nm) in crown glass which has a refractive index of 1.52 (no units).

$$n=\frac{{\mathrm{sin\; \theta }}_1}{{\mathrm{sin\; \theta }}_2}=\frac{{\lambda }_1}{{\lambda }_2}=\frac{v_1}{v_2}$$

In this case we need to use:

$$n=\frac{{\lambda }_1}{{\lambda }_2}$$

Which gives us the following substitution

$$\mathrm{1.52}=\frac{\mathrm{509}}{{\lambda }_2}$$

Solving this equation gives us:
λ₂ = 335 nm which is in the ultraviolet part of the electromagnetic spectrum

---

Interactive examples and solution

Attempt to solve the question yourself before clicking the solve button!

The refractive index of a material is . Determine the speed of light in this material.
(Numbers in the box and solution may be displyed in the computer form where e+8 represents x 10⁸)

---

The wavelength of light in a medium is nm and the refractive index of the material is . Determine the speed of light in air.

---

The speed of light in a material is m s^-1. Calculate the angle of refraction for a ray coming from air striking the material with an angle of incidence of °.

---

Frequency and Refractive Index

When white light passes through a triangular prism it is possibe to generate a rainbow as shown in the diagram below.

The red light with the longest wavelength and lowest frequency bends the least and the violet light with the shortest wavelenght and highest frequency bends the most. This shows us that the refractive indices for colours depends on the frequency of the light. Higher frequency waves are slowed down more as they interact with the electrons in the material and so they have a higher refractive index. This dispersion of which light can only occur because the refractive index of the light is dependent on its frequency.