Higher Physics

Wave particle duality

Classical physics does not work

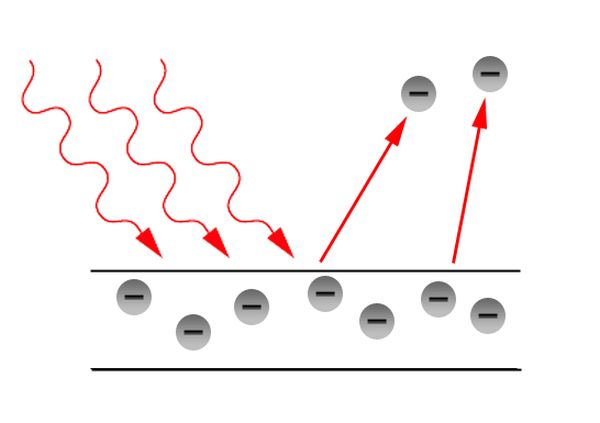
When light strikes the surface of a metal it is possible for the light to eject electrons. Classical physics would equate the energy of the light to be determined by the intensity of the light. This would mean that high intensity, very bright light, would eject electrons from the surface of any metal. This is not what we find experimentally. The frequency of light is the key variable which determines if electrons are emitted from the surface of a metal. Light has to have a high enough frequency for electrons to be emitted. Why?

Light is a Particle

Einstein was the scientist who came up with the solution to the problem that the frequency of light determined if there was electron emission from the surface of a metal. He proposed that light was composed of particles where their energy was dependent on the frequency of the light, and not the amplitude. He used the work of Max Planck who had already proposed the equation E = hf to solve the ultraviolet catastrophe. This has resulted in physicists understanding that light is quantised. The small energy packets whose energy is based on the frequency are called photons, and therefore light behaves as a particle.

$$E=\mathrm{hf}$$

This equation is one of the most important in modern physics.

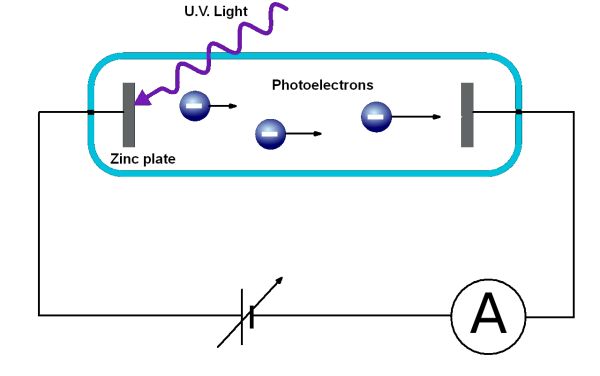
The minimum energy to remove an electron from the surface of a metal is known as the Work Function of the metal. This requires light of a threshold frequency, f₀.

When light of a frequency greater than the threshold frequency strikes the surface of a metal the remaining energy of the light can be converted to kinetic energy in the electron. This will only occur for electrons right at the surface of the metal. Therefore they will have the maximum possible kinetic energy. The amount of kinetic energy can be determined by providing an electric field that will repel emitted electrons. See the diagram above. When the electric field is large enough to stop electrons with the maximum kinetic energy the current in the circuit will drop to zero. This is called the stopping potential. The relationship to determine the kinetic energy is given by:

$$E_k=\mathrm{hf}-{\mathrm{hf}}_0$$

Where:

• E_k is the kinetic energy of the electron
• h is Planck's Constant
• f is the frequency of the incident light
• f₀ is the frequency of light supplying energy equivalent to the work function of the metal

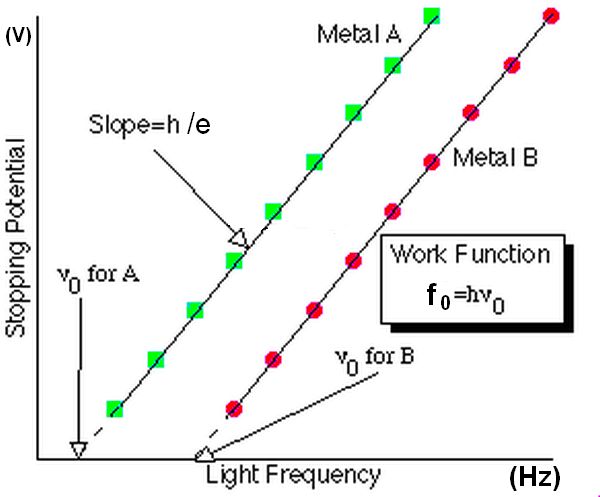
Effectively we are using conservation of energy to convert kinetic energy to work done on stopping the electron. This allows us to plot stopping potentials against frequency of light. This allows us to determine the work function of the metal.

$$E_k=\frac{1}{2}{\mathrm{mv}}^2=\mathrm{QV}=\mathrm{hf}-{\mathrm{hf}}_0$$

The charge on the electron is known as well as the frequencies of light used and the stopping potential. The threshold frequency is a fixed value specific to each metal. The plot produces a straight line with a slope equivalent to h/e and where the line crosses the x-axis we can determine the threshold frequency (f₀).

Light is a wave

For several hundred years scientists were aware that light had wave properties. This was most cleary shown in the superposition of coherent waves. The classic experiment demonstating this is known as Young's Double Slit Experiment.

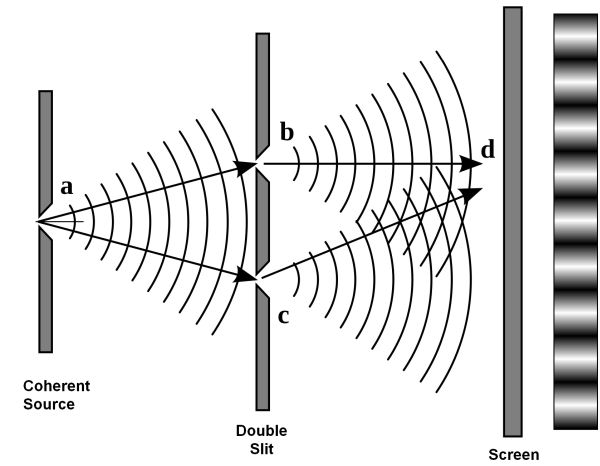
The diffraction of light through the two slits leads to an interference pattern which you can read more about in the section on interference.

Interference