Higher Physics

The Expanding Universe

The Doppler Effect

When you hear the siren of an emergency vehicle approaching to you it has a higher pitch than when it has passed and is travelling away from you. The actual frequency of the sound can be heard when the vehicle is stationary, and when it is directly opposite you as it passes. Mathematically it is possible to determine the actual changes in frequency of the wave. This effect is known as the Doppler Effect. It is something that all wave types experience.

Ambulance approaching = higher pitch
Ambulance opposite = actual pitch
Ambulance moving away = lower pitch

Image showing wavefronts of a non moving wave, and the same one moving

 

Below is the equation for the Doppler effect

$$f_0=f_s\left(\frac{v}{v \pm v_s}\right)$$
Where
f₀ is the change in frequency
f_s is the frequency of the original wave
v is the velocity of the wave (the speed of sound, or the speed of light)
v_s is the speed of the source

You wll notice that there is a ± on the bottom line of the fraction. This relates to whether the wave is approaching you or going away from you.
Use the - when the wave is approacing you (bottom line of fraction is smaller therefore f₀ is greater)
Use the + when the wave is going away from you (bottom line is larger therefore f₀ is lower)
It is important to realise that this change of frequency occurs for all types of waves that are moving, including light.

In the animation below you can see and hear the doppler effect with a light aircraft passing.

Frequency calculations

An siren with a frequency of 1000 Hz is being emitted from a vehicle which is approaching at 15 m/s.
(a)  What is the frequency heard by the person standing still?
(b)  What is the frequency of the sound when the vehicle is moving away from the person at 15 m/s?
E E S S U U
(a)
f_s = 1000 Hz
v = 330 m/s
v_s = 15 m/s
Since the sound is approaching it will be at a higher frequency and so we use the following equation: $$f_0=f_s\left(\frac{v}{v-v_s}\right)$$ $$f_0=\mathrm{1000\; Hz}\left(\frac{\mathrm{330\; m/s}}{\mathrm{330\; m/s}-\mathrm{15\; m/s}}\right)$$ $$f_0=\mathrm{1047\; Hz}$$ $$\frac{f_0=\mathrm{1050\; Hz}}{\mathrm{}}$$
E E S S U U
(b)
f_s = 1000 Hz
v = 330 m/s
v_s = 15 m/s
Since the sound is receeding it will be at a lower frequency and so we use the following equation: $$f_0=f_s\left(\frac{v}{v+v_s}\right)$$ $$f_0=\mathrm{1000\; Hz}\left(\frac{\mathrm{330\; m/s}}{\mathrm{330\; m/s}+\mathrm{15\; m/s}}\right)$$ $$f_0=\mathrm{956.5\; Hz}$$ $$\frac{f_0=\mathrm{957\; Hz}}{\mathrm{}}$$
An observer hears a 5000 Hz wave with a frequency of 5500 Hz as it approaches her. What speed is the object moving the at?
E E S S U U
f₀ = 5500 Hz
f_s = 5000 Hz
v = 330 m/s
v_s = ? m/s
Since the sound is approaching it will be at a higher frequency and so we use the following equation: $$f_0=f_s\left(\frac{v}{v-v_s}\right)$$ $$\mathrm{5500\; Hz}=\mathrm{5000\; Hz}\left(\frac{\mathrm{330\; m/s}}{\mathrm{330\; m/s}-v_s}\right)$$ $$v_s=\mathrm{32.7\; m/s}$$ $$\frac{v_s=\mathrm{32.7\; m/s}}{\mathrm{}}$$

The size of the frequency shift depends on the speed of the source. This will be an important point to remember when we consider more details about the expansion of the universe and the use of red shift to give us information on how far away galaxies are.

Measuring Distance

How do we measure distances in space? Measurement takes time because we use Earth's orbit around the Sun to make measurements.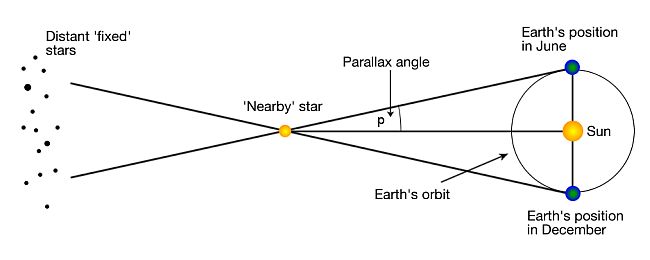

Note that in the animation above the nearer the star is to the Earth, the greater the backwards and forwards motion of that star with respect to the very distant fixed points of light. In the old days these fixed points would have been called stars, but now we know that many of them are actually galaxies that are very very far away. When we know the mid point of the star's oscillating position it is then possible to determine the angle that it makes at the maximum displacement and by using trigonometry we can calculate the distance the star is from Earth.

The Hubble space telescope is capable of measuring a parallax angle of 0.04 arc seconds. Remember that there are 60 minutes in a degree and 60 seconds in a minute. So the value of 0.04 arc seconds is aproximately 1.1 × 10^-5 of a degree. This is about one thousand times more accurate than can be detected by the human eye. Further improvements to the Hubble Space Telescope means that it can now measure to a distance of approximately 8000 ly using parallax and properties of the image sensors in the cameras.

Expanding Universe

Consider the emission spectra from a star. We know the frequency of the hydrogen lines from laboratory experiments and our sun. The one of greatest interest is at 1420.4 MHz. This has a wavelength of around 21 cm and can be detected by radio telescopes. If the suns and galaxies in the universe are stationary with respect to the earth as was thought in the past the only evidence of the Doppler effect would be from the motion of the earth in its orbit around the sun.
On looking at the spectra from stars and galaxies Edwin Hubble discovered that the further away a galaxy is from us the greater the doppler effect on the light that is recieved here on earth. This suggests that the furthest away objects are moving the fastest, and closer objects are moving more slowly.
Let us look at the change in frequency of the 1420.4 MHz hydrogen spectrum line. A galaxy is travelling at 1000 km/s and has been measured as being 50 Mly away. What is the frequency of the 1420.4 MHz line from the hydrogen spectrum.
f_s = 1420.4 x 10⁶ Hz
v = 3.0 x 10⁸ m/s
v_s = 1000 x 10³ m/s
Since the light is receeding it will be at a lower frequency and so we use the following equation: $$f_0=f_s\left(\frac{v}{v+v_s}\right)$$ $$f_0={\mathrm{1420.4\; x\; 10}}^6\left(\frac{{\mathrm{3.0\; x\; 10}}^8}{{\mathrm{3.0\; x\; 10}}^8+{\mathrm{1000\; x\; 10}}^3}\right)$$ $$f_0={\mathrm{1415.7\; x\; 10}}^6$$ $$\frac{f_0=\mathrm{1415.7\; MHz}}{\mathrm{}}$$
As can be seen from the result, the frequency is lower, and this is called red shift as the wavelength is shifted to a longer (redder) wavelength.
Clearly, scientists measure the values of the frequency of the hydrogen line and then calculate the recessional velocity, rather than the calculation we just carried out.
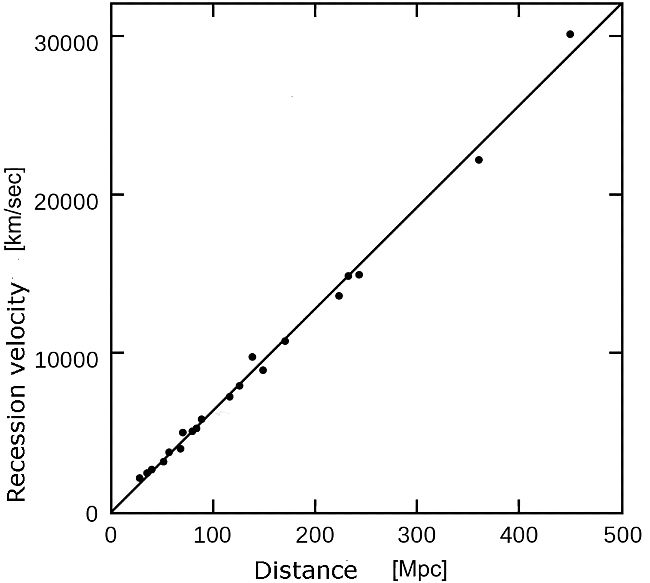
Over time the frequency shift (and therefore the recessional velocity) and distance of many galaxies has been measured. The results have been plotted on a graph and it is shown below.

Nasa have a good graphic on how the vaue of the Hubble constant can be determined. Please se below.
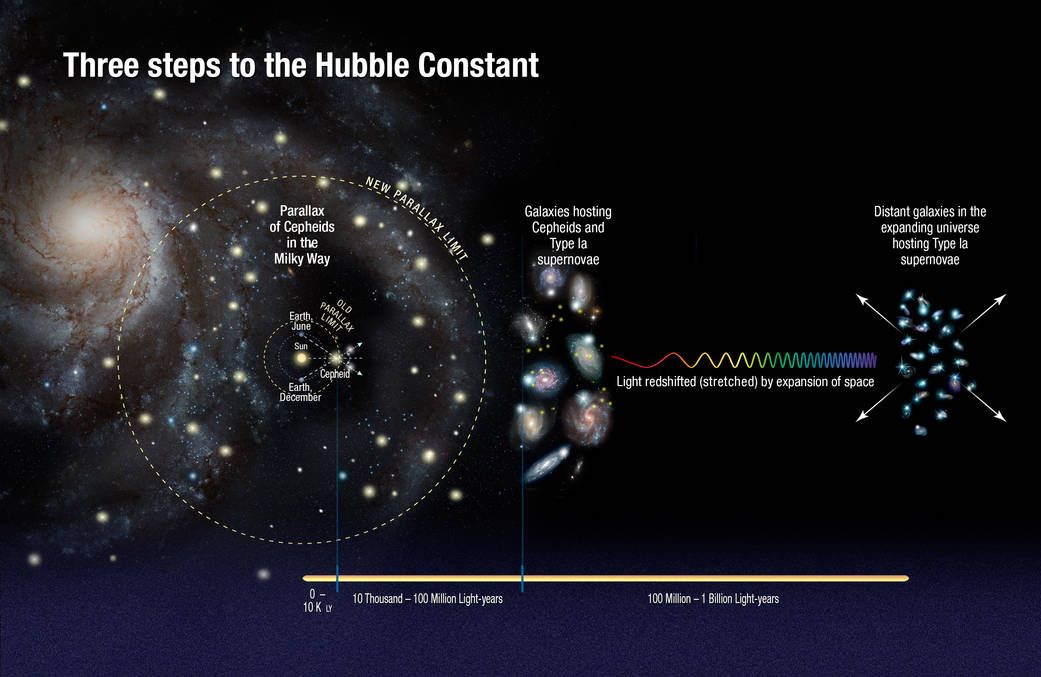
The link for this graphic is Nasa Link
The current value of the Hubble constant is estimated to be 73.8 km/sec/Mpc ± 2.4 km/sec/Mpc.

Red-Shift

In the animation below each of the stars represents a galaxy. Initially the galaxies are all together in the same spot. Space begins to expand and the galaxies move with different speeds. As time progresses they get further and further apart. The galaxy that is moving the fastest is furthest away from the start position.

As can be seen above the colour of light from the galaxies changes because they are moving with different speeds. Below is another animation which shows how the frequencies of known spectral lines change with how distant a galaxy is from our solar system. The changing of the frequency of light is called redshift, and is observed for most galaxies. This is because most galaxies are moving away from ours. If a galaxy is moving towards us the line spectrum for that galaxy would be blueshifted.

Red shift is only measurable for objects that are very far away and moving at very high speeds.

The redshift of a galaxy is the change in wavelength divided by the emitted wavelength. $$z=\frac{{\lambda }_{\mathrm{observed}}-{\lambda }_{\mathrm{rest}}}{{\lambda }_{\mathrm{rest}}}$$
Where:
z = redshift, unusual as it has no unit, it is just a number
λ_observed = wavelength observed on Earth
λ_rest = wavelength observed when source is not moving relative to Earth
If z is positive then λ_o > λ_rest the wavelength has been redshifted and the galaxy is moving away from us.
If < strong>z is negative then λ_o < λ_rest the wavelength has been blueshifted and the galaxy is moving towards to us.
For slowly moving galaxies, redshift is the ratio of the velocity of the galaxy to the velocity of light. $$z=\frac{v}{c}$$
Say a galaxy emits a characteristic spectral line at 210 nm when it is measured as 640 nm here on earth, we can calulate the red shift as:
E E S S U U
λ_observed = 640 nm
λ_rest = 210 nm $$z=\frac{{\lambda }_{\mathrm{observed}}-{\lambda }_{\mathrm{rest}}}{{\lambda }_{\mathrm{rest}}}$$ $$z=\frac{\mathrm{640\; nm}-\mathrm{210\; nm}}{\mathrm{210\; nm}}$$ $$z=2.05$$ $$\frac{z=\mathrm{2.05\; no\; units}}{\mathrm{}}$$

This graph shows a directly proportional relationship between recession velocity and the distance the object is from us. This is Hubble's Law and can be expressed in equation form: $$v=H_{\mathrm{0 }}d$$
The expansion includes galaxies in all directions from the earth. Since this is the case, what happens when the clock is wound backwards? All the galaxies converge to a single point. This lead to the idea of a "big bang", where the universe began, and has been expanding ever since. As measurements have improved this has led to a start of the universe 13.8 billion years.
The current value for H₀ is 2.3 x 10^-18 s^-1 when v is measured in metres per second and distance measured in metres.

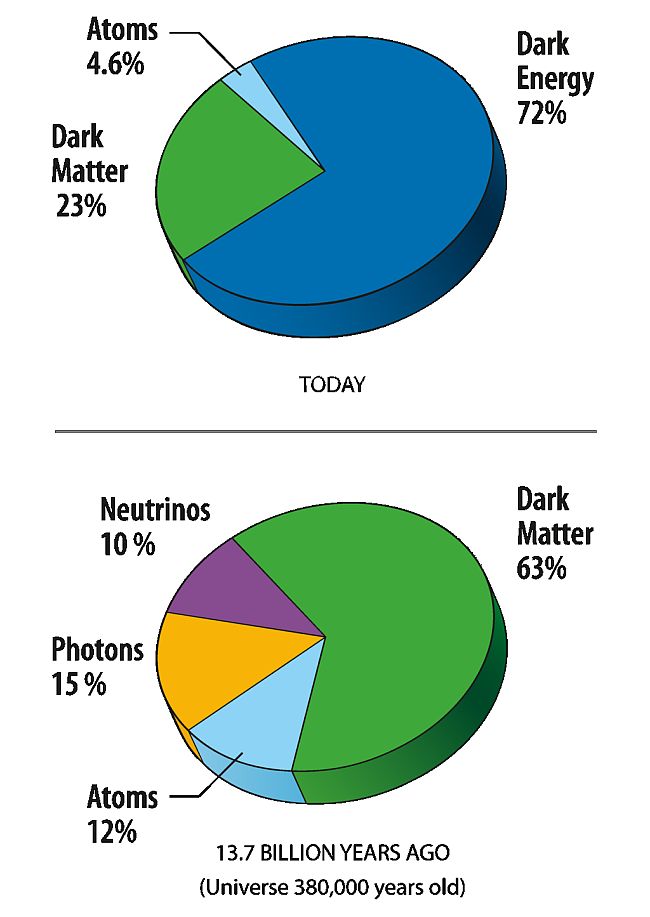
Expanding Universe Evidence

Hubble's law and the spectroscopic data it is based on provide strong evidence for the expanding universe.
Considering the energies present at the big bang there should be a uniform energy that has been stretched out from the expansion. At around 380,000 years after the Big Bang the universe was cool enough for the formation of atoms and become transparent. The oldest light in the universe dates from this time. In 1964 radio astronomers Robert Wilson and Arno Penzias discovered Cosmic Microwave Background Radiation (CMBR) which is the stretched out remains of that initial light. It is found uniformly in all directions iin space.

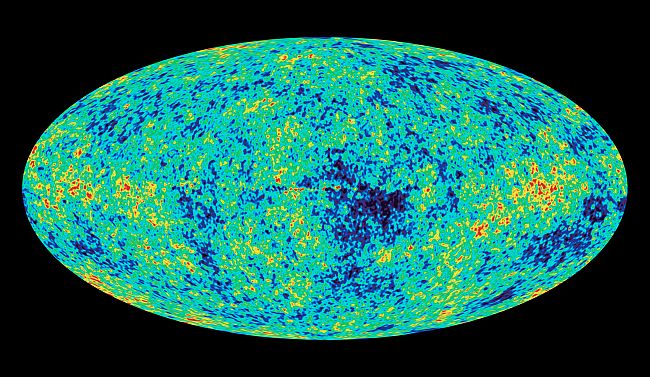
Cosmic Background Microwave Radiation Map

Evidence also shows that the expansion of the universe is not constant. The current rate of expansion is accelerating.

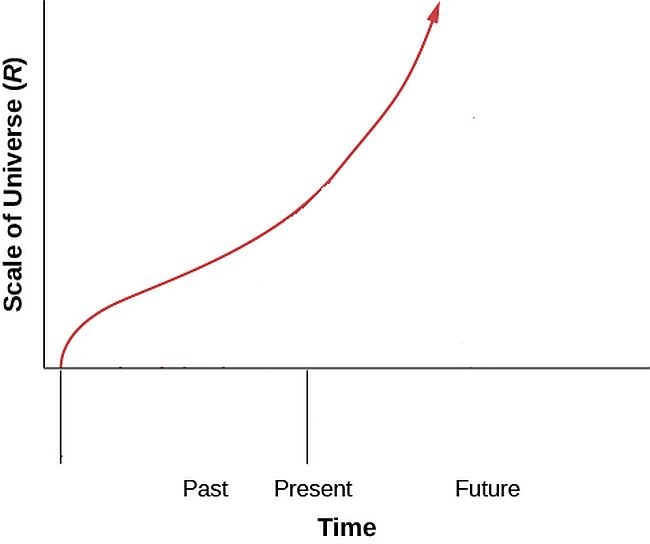
It is important to note that dark energy is not bound by the laws of relativity determined by Einstein. There is therefore no known upper limit for the rate of expansion and expansion can happen at a rate faster than the speed of light.

Mass of Galaxy

How can we determine the mass of the galaxy? With an understanding of Newton's Universal Law of Gravitation it is possible to calculate the mass of stars using their orbital velocities. Remember that most stars are binary systems. We can also measure the orbital velocity around the centre of our galaxy. In doing so we assume that the motion is almost entirely dependant on the matter inside the galaxy. A star with greater mass will have a greater gravitational attraction and therefore a higher orbital velocity.
The current estimate of the mass of our galaxy is between 6 x 10⁵³ and 10 x 10⁵³ kg. The mass of our sun is approximately 1 x 10²⁴ kg
This estimate of mass is much greater than the visible matter that we are able to observe. In order to deal with this discrepancy between experimental results and theory it has been proposed that there is a type of matter that does not emit electromagnetic radiation. This type of matter is called Dark Matter This type of matter makes up most of the matter in the galaxy, and in the universe. Detecting what it is is very challenging because it does not emit electromagnetic radiation, which is what we have used to discover details of the universe so far.