Higher Physics

Forces, energy and power

Forces

Forces are vectors.
A force will have one or more of three effects when it acts on an object

The object will accelerate

The object will change direction

The object will change shape

In all situations where the forces balance, the resulting force/net force will be 0 N.
In any situation where the net force is not 0 N one or more of the three effects listed above will take place.
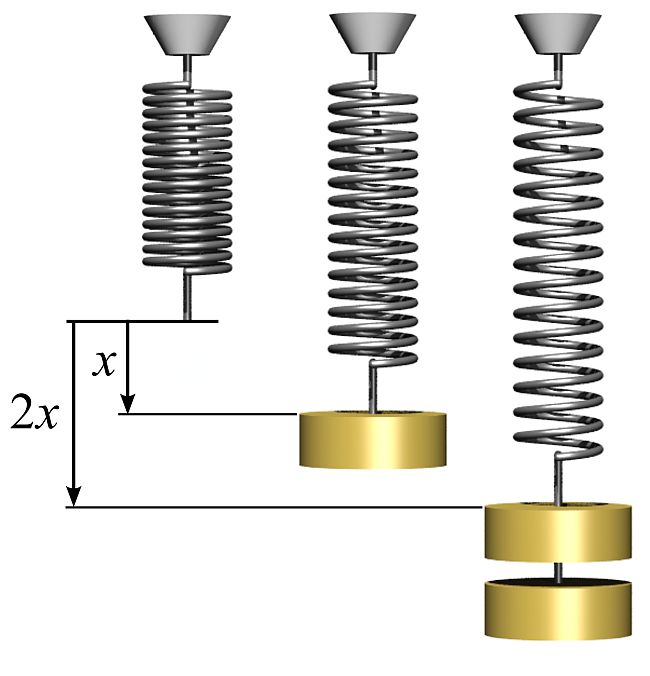
Consider a spring with a mass added to it. The spring has an unbalanced weight force and so it stretches. Ths is a change of shape. Eventually the length of the spring no longer increases and the unbalanced weight force is counterbalanced by the increased length of the spring. When the two forces are balanced we have returned to a zero net force situation and no further change of shape occurs.


Which of the two objects in the diagram below has the larger force acting upon it?

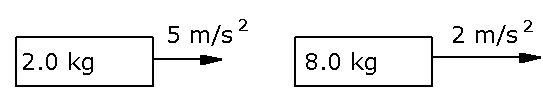
The smaller mass may have a larger acceleration, but the larger mass object requires more force than the smaller one for it to accelerate at 2 m/s².
We can calculate the actual forces by using the equation: $$F=\mathrm{ma}$$
For the 2.0 kg mass $$F=\mathrm{ma}$$ $$F=\mathrm{2.0\times 5}$$ $$F=\mathrm{10\; N}$$
For the 8 kg mass $$F=\mathrm{ma}$$ $$F=\mathrm{8.0\times \; 2}$$ $$F=\mathrm{16\; N}$$

---

What is the acceleration of the skier

Try and solve the question before clicking the solve button to check your answer

A skier is starting to accelerate down the ski slope. The net force acting on them in the direction of travel is N. The skier has a mass of kg. Calculate the acceleration of the skier.

---

When a ball is dropped off a cliff the force of gravity causes it to accelerate. In ideal circumstances we can ignore air resistance. For most of the examples and questions in this course we will consider the situation as ideal. We must remember that air resistance produces a force opposite to th direction of travel, and in reality will result in slower accelerations than ideal behaviour. In the absence of air resistance all objects fal with the same acceleration irrespective of their mass.

You can click on the image below to see the video on YouTube

As can be seen in the video linked above feathers and balls drop with the same acceleration when there is no air resistance.
When air resistance is present we see the action of another force, opposing the fall of both the feather and the ball. The feather experiences a much greater air resistance and is therefore opposed by a greater force than the ball. The result is that it accelerates towards the surface much more slowly than the ball. This is due to the net force being smaller, not the gravitational attraction.
Many people often confuse this and think that heavier objects fall faster than light ones, but since the time of Gallileo we have known that this is not the case. Many cartoons rely upon the heavier things fall faster concept in their presentation of reality. This helps to reinforce a physics misconception from a very young age.

The acceleration of any object, near the surface of the earth, will be 9.8 ms^-2 due to the force of gravity. All objects accelearate at the same rate due to the force of gravity.

The name of the force acting on an object due to the gravitational field is called weight. Often students can find this confusing because in every day language weight is measured in kg. In physics this is not the definition of weight, which is a force. In physics weight is measured in newtons because it is a force. The relationship between weight, mass and the gravitational field strenght is given by:

$$W=\mathrm{mg}$$

Where
W = weight (N)
m = mass (kg)
g = gravitational field strength (N kg^-1

This is the equation we must always use when calculating weight values. The SQA examiners do not allow the use of F = ma in weight calculations.

On the surface of Mars the gravitational field strenght is 3.7 N kg^-1. Calculate the weight of the 1030 kg Mars Rover on Mars?

$$W=\mathrm{mg}$$ $$W=\mathrm{1030\; \times \; 3.7}$$ $$W=\mathrm{3810\; N}$$

---

What is the weight of a space probe

Try and solve the question before clicking the solve button to check your answer

The gravitational field strength at the surface of a planet is N kg^-1. A space probe with a mass of kg lands on the surface.
(a) Calculate the weight of the of the space probe on the planet.
(b) Determine the weight of the space probe on Earth.

---

What is the gravitational strenght of an object in space

Try and solve the question before clicking the solve button to check your answer

The weight of a space probe near the surface of an object is N . The mass of the space probe on Earth was kg. Calculate the gravitational field strength of the object near the space probe.

---

Newton's First Law

Any object that is stationary or moving in a straight line at a constant velocity will continue to be stationary, or moving in a straight line at a constant velocity unless acted upon by a force.
This is not intuitive because we normally experience friction forces, which oppose the direction of motion. Reducing friction forces allows us to see the validity of this first law.

Swing an object around in a circle above your head with an even speed. When you let the object go it ceases travelling in a circular motion. Instead it travels in a straight line as it heads away from you. This is becuase there are no longer any forces causing it to change direction in the plane that you were swinging it. From above, the object will move in a straight line. This is an example of Newton's First Law.

Newtons's First and Second Laws

Friction

Friction is a resistive force which always opposes the direction of motion of an object. It is the result of the imperfections in the smoothness of any surface. The amount of friction experienced by an object depends on the roughness of the surface and the weight of the object. In this course static and dynamic friction are not

Gravitational Field Strength

The gravitational field strength is defined as the force (in Netowns) per unit mass (kg). For this planet, near the surface we regard this field as a uniform field with a value of 9.8 Nkg^-1.
This field strength leads to an acceleration of 9.8 ms^-2 for all objects near the surface. In the absence of significant effects from air resistance we can approximate the vertical motion of all objects to be an acceleration of 9.8 ms^-2

Air Resistance

As an object accelerates falling through the air it has to push the air in front of it out of the way. The air exerts a resistive force on the falling object which is called air resistance. The faster the object is falling the greater the value of this force.

Terminal Velocity

When the force upwards due to air resistance in equal and opposite to the downard force from the gravitational field we are in a balanced forces situation. In this cas the object is falling with a constnt velocity which we call the terminal velocity of the object.
Graphing Terminal velocity for a parachutist can be seen below. Let us break this down into separate sections.
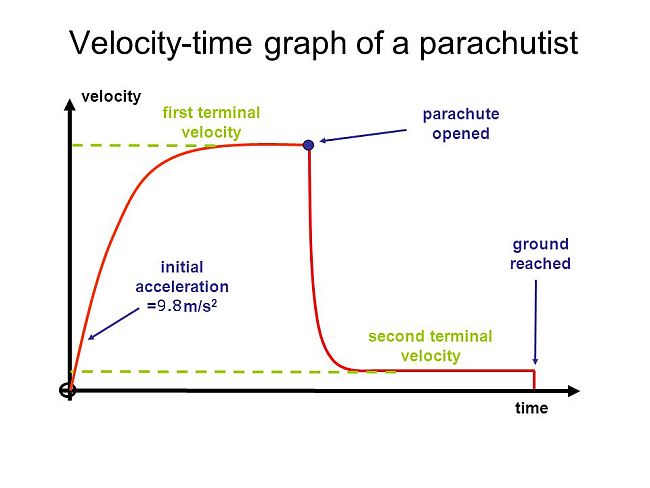
Initial Acceleration
The initial acceleration results in the parachutist accelerating at 9.8 ms^-2 because there is relatively low air resistance. The air resistance force arrow is quit small.

Slowing acceleration (curved part)
As the parachutist gains speed the air resistance increases. This is because they are trying to push a greater volume of air out of the way each second. The air resistance force arrow is larger, but still smaller that the weight force.

Terminal Velocity
As can be seen from the graph ther comes a point at which the parachutist no longer accelerates and the graph is now horizontal. This indicates that the person is not accelerating, but that they have a fixed speed. This is because the downward force of weight is being balanced by the opposite force of air resistance. When these two forces are balanced we state that the object is moving with its terminal velocity. The two force arrows are the same length but in opposite directions.

Parachute Opens
When the parachute is opened there is an immediate acceleration against the downwards direction of the parachutist. Therefore the parachitist is slowing down. As they slow down the increased air resistance is balanced by at a slower rate of descent and so a new lower terminal velocity is reached. This velocity is slow enough to ensure the parachutist is not hurt when they land. The air resistance force arrow increases dramatically.

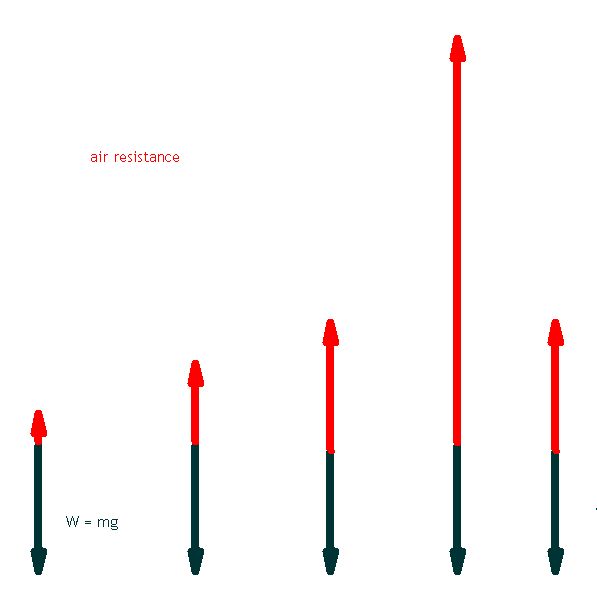
Velocity time graph with air resistance
The first section of the graph above is typical of a velocity time graph for an object in freefall. Due to the increasing resistance of the air as the object increases its speed, the rate of acceleration slows down. When the two forces, gravitational acelleration/air resistance, balance each other there is no longer any acceleration and the object has reached terminal velocity. The two force arrows are the same size but opposite in direction.

Newton's First Law

This law states that an object in motion, or at rest, will stay in motion, or at rest, unless acted upon by a force. This is most easily illustrated by thinking about an object in deep space where there is nothing else close by. The object will carry on moving in a straight line with a constant velocity, or stay at rest if it was at rest. When a force acts upon it there will either be a change of velocity, change of direction or a change of shape.
This is not intuitive. On earth we always have the presence of friction which is a force that opposes the direction of motion of an object. It took a great leap in thinking to imagine a world without friction for Newton to devise this first law.

Newton's Second Law

The product of the mass of an object and its acceleration is direcly proportional to the force acting on the object.
Alternatively it could be said that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the direction of the net force, and inversely proportional to the mass of the object.
This is most simply put in an equation:
$$F=\mathrm{ma}$$

Where:
F - Force (N)
m - mass (kg)
a - acceleration (ms^-2)

Consider an object with a mass of 500 kg. What force would be required to accelerate the object 10 ms^-2?
F = ?
m = 500 (kg)
a = 10 (ms^-2)
$$F=500\times 10$$ $$F=\mathrm{5000\; N}$$

In all situations when there is no net force, i.e. F_net = 0 N, there will be no acceleration. The object will carry on moving in a straight line at a constant velocity, or will remain at rest.
When there is a net force there will be an acceleration. This will either cause a change in speed of the object (faster or slower) or a change in direction of the object. For most situations we ignore changes of shape at this level.
Consider an object with a mass of 5 kg experienceing a force of 40 N. What will the acceleration of the object be? $$F=\mathrm{ma}$$
Where F = 40 N
m = 5 kg
a = ? $$\mathrm{40\; N}=\mathrm{5\; kg}\times a$$ $$a=8{\mathrm{ms}}^{-2}$$

Resolution of a vector into two perpendicular components.

In National 5 physics we added two vectors that were are right angles, and learnt the use of pythagoras and trigonometry to help us solve these questions. In higher two or more vectors may be give, which are not at right angles to each other, and now we need to be able to add vectors in this situation. An example is when we wish to determine the velocity of a plane experienceing a crosswind. If you look at the diagram below, you will see an example of this type of vector addition.

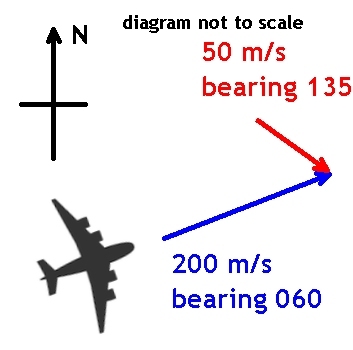
We can see that these vectors are not at 90 degrees to each other and so we have to work out how to add them. This can be achieved by breaking up each vector into its vertical and horizontal components. The components can then be added together and the final resultant vector calculated. Look at the broken arrows in the diagram below. These broken arrows are the horizontal and vertical components of the initial vectors.

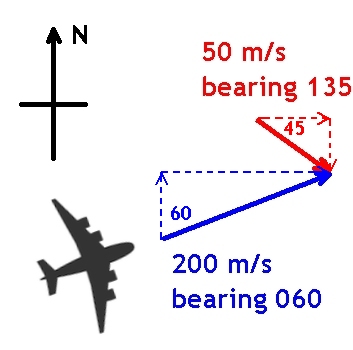
Let us first work out the components of the velocity of the plane which is travelling at 200 m/s on a bearing of 060.

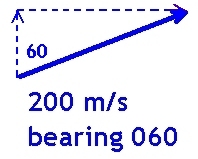
In the north direction (vertical component) this can be calculated using 200 cos(60) = 100 m s^-1
In the east direction (horizontal component) this can be calculated using 200 sin(60) = 173 m s^-1

Next let us calculate the components of the wind vector

In the south direction (vertical component) this can be calculated using -50 cos(45) = -35.4 m s^-1
The wind vertical component is acting south and so it is given a negative value, because we have already assigned north to be the positive direction.
In the east direction (horizontal component) this can be calculated using 50 sin(45) = 35.4 m s^-1

Now we can add the vertical components to get the total vertical size of the final velocity.
Final vertical velocity component = 100 + (-35.4) = 64.6 m s^-1

Next we will add the horizontal components together to get the total horizontal size of the final velocity
Final horizontal velocity component = 173 + 35.4 = 208.4 m s^-1

We must now combine these two components to get the resultant velocity
Remember that they are perpendicular and so form a right angled trinagle as can be seen in the image below:

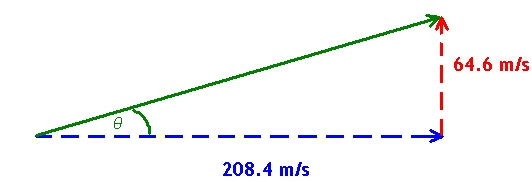
The magnitude of the velocity is can be calculated using pythagoras:

$$v^2={\mathrm{208.4}}^2+{\mathrm{64.6}}^2$$ $$v=\sqrt{{\mathrm{208.4}}^2+{\mathrm{64.6}}^2}$$ $$v=\mathrm{218.2}{\mathrm{ m\; s}}^{\mathrm{-1}}$$

v = 218 m s^-1

This is a velocity and so we need to work out the direction it is travelling. We can do this using trigonometry.

The angle that we want to calculate is the angle b. This can be calculated using the inverse tan function.

$$b={\tan }^{\mathrm{-1}}\left(\frac{\mathrm{208.4}}{\mathrm{64.6}}\right)$$ $$b=\mathrm{73°}$$

Therefore the final result is that the plane is travelling with a velocity of 218 m s^-1 on a bearing of 073.

Work and Conservation of energy

When a force is useed to move an object the amount of work done is given by the following equation:
$$E_w=\mathrm{Fd}$$ Where

• W = work done (in the direction of the force)
• F = the force applied
• d = distance moved in the direction of the applied force

Example Consider a car of mass 1500 kg which is going to be crushed. It is lifted 10 m by a crane off the ground. How much work is done agains gravity by the crane?
$$E_w=\mathrm{Fd}$$ In this case the force is the weight of the car.
W = 1500 x 9.8 = 14,700 N $$E_w=\mathrm{14700}x\mathrm{10}$$ $$E_w=\mathrm{147\; kJ}$$ How much work is done against gravity when the crane shifts the object 20 m to the left?
We have to remember the definition of work done - force x the distance moved in the direction of the force.
In this case there is no work done against gravity, because the movementf of the car is at 90 degrees to the force of gravity acting upon it.

$$E_w=\mathrm{0\; J}$$ If there is a friction force acting on the crane of 150N as the car moves left, what is the work done against friction? $$E_w=\mathrm{Fd}$$ $$E_w=\mathrm{150\; x\; 20}$$ $$E_w=\mathrm{3.0\; kJ}$$ How much power did the crane use if the movement to the left took 25 seconds?
$$P=\frac{E}{t}$$ $$P=\frac{\mathrm{3000}}{\mathrm{25}}$$ $$P=\mathrm{120\; W}$$