Gravitation

Experiment to determine the acceleration of a falling object

It is possible to determine the acceleration of a falling object by a simple experiment.
Determining the acceleration for a trolley on a ramp with a low angle produces a graph with a straight line. If the distance between the light gates is exaclty one meter then a simplification can be used based on the following diagram.

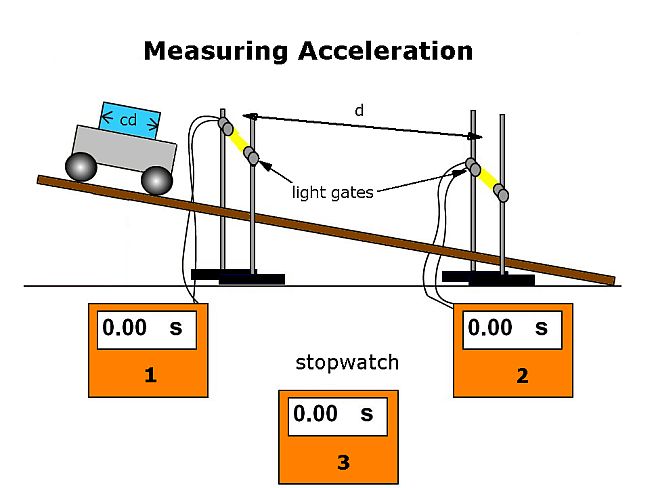
The time taken to pass between the two light gates can be recorded along with the initial velocity and final velocity of the trolley (determined by the data logger)

$$a=\frac{\mathrm{v\; -\; u}}{\mathrm{t}}$$

This can be used to determine the average acceleration of the trolley. By increasing the angle we can get several results which would allow us to determine a value at a ramp angle of 90°. This should be the same acceleration as the gravitational filed strength. It is often smaller due to friction effects in the experiment.

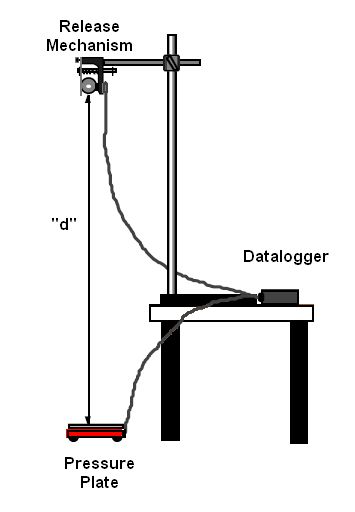
To determine the acceleration of a falling object an experiment with either a video and known drop height, or one where a timer starts the moment the object falls and stops the moment it lands could be used. In both cases the initial vertical velocity, u = 0 m/s. This simplifies the equation from

$$s=\mathrm{ut}+\frac{1}{2}a{t}^2$$

to

$$s=\frac{1}{2}a{t}^2$$

As long as we know the drop distance, and the electronic timer calculates the time to a sufficient degree of accuracy, the acceleration due to the gravitational field can be calculated. The eperiment should be carried out at different heights, "d" and repeats should be carried out to determine the random uncertainty in the results.

Providing the drop height is known accurately this experiment will generally give an acceleration due to g of about 9.7 to 9.8

Projectile Motion

A projectile is an object that has motion which can be resolved into two components.

The horizontal component has a constant velocity
The vertical component has a constant acceleration downwards

On earth, the gravitational field strength is 9.8 N/kg. The object therefore accelerates at
9.8 ms^-2 downwards
For an object that is initially heading upwards, the acceleration will cause the object to slow down.
For an object initially moving horizontally it will accelerate downwards while moving with a constant horizontal velocity.
The image below shows the horizontal motion, and the effect of the constant acceleration on a projectile

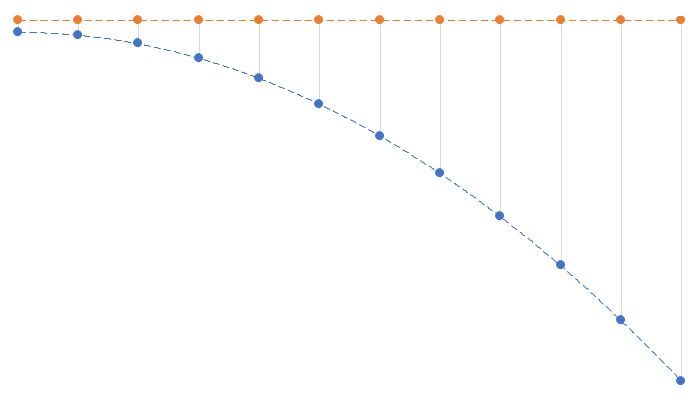
A projectile can be launched at an angle other than horizontally. When dealing with cases like this the vector describing the initial motion can be resolved into the horizontal and vertical components. When this is done, the horizontal component descirbes the constant velocity of the object. The vertical component describes the constant acceleration of the object.

Satellite Free Fall

Consider projectile motion and how an object accelerates under the influence of a gravitational force. If the object is moving fast enough hotizntally this velocity keeps the falling object the same distance from the curved surface. With an atmosphere the air resistance will cause the the gradual decrease of the horizontal velocity. The object will then fall to the surface.
In space, outside our atmosphere, there is no air resistance and so a sattelite continues to travel in an orbit. This means that the satellite is in free fall. It accelerates constantly towards the surface, but the horizontal componenet of the velocity is fast enough to make sure it gets no closer to the surface due to the curved orbital path.

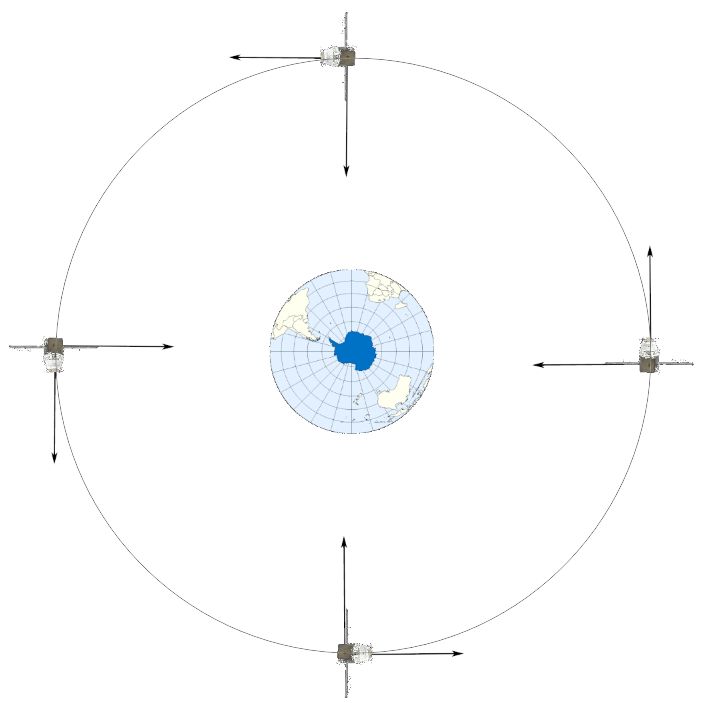
Just as a satellite orbits a planet in freefall, a planet orbits the sun in freefall.

Resolution of initial velocity into horizontal and vertical components

Consider the following situation, where a rugby ball is being kicked along the pitch. The initial velocity of the ball is 23 ms^-1 at an angle of 41 degrees above horizontal.

We can use the following relationships to determine the horizontal and vertical components of the flight.
Horizontal = 23 cos(41) = 17 ms^-1
Vertical = 23 sin(41) = 15 ms^-1

Look at the expanded image of the initial force.

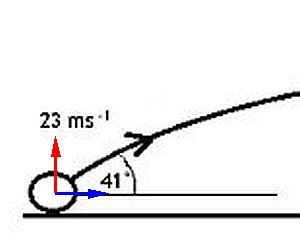
Horizontal velocity

The horizontal velocity is only subject to air resistance. An assumption is made that this is too small to have an effect over the small distances involved. This means that the horizontal velocity is constant. The value will always be given by:

F cos(θ)

Vertical velocity

The vertical velocity is subjected to a constant force from the gravitational attraction of the planet. On earth the value of the attraction is 9.8 N/kg. On another planet e.g. Mars it is 3.7 N/kg. The gravitational field strenght will affect the value of the acceleration experienced by the object.
A constant force will produce constant acceleration towards the planet. There are three options that will appear most frequently.

Vertical launch
When an object is vertically projected there is only the vertical component to consider. This component is subject to a vertical force in the opposite direction.

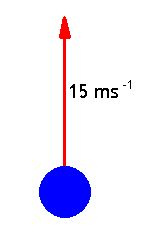
We can determine how long it takes to reach its maximum height.
s = ?
u = 15 m/s
v = 0 m/s (because at the maximum height it has stopped moving upwards)
a = -9.8 m/s² (remember the direction is opposite to the upwards direction of the launched item therefore it requires a negative sign)
t = ?

v = u + at
0 m/s = 15 m/s - (-9.8 m/s²)t
t = 15/9.8 = 1.53 s
t = 1.5 s (Don't forget to round to the same number of digits as the numbers in the question)

We can also work out how high the object went.
Using the original information from the equation we can use the following equation:
v² = u² + 2 as
0 = 15² + 2 x (-9.8) x s
s = 11.48 m
s = 11.5 m

Upwards angled launch
With the angle of launch neasured from the horizontal we need to remember that the vertical comonent of this is:
F sin(θ)
s = ?
u = F sin(θ)
v = 0 m/s (because at the maximum height it has stopped moving upwards)
a = -9.8 m/s² (remember the direction is opposite to the upwards direction of the launched item therefore it requires a negative sign)
t = ?
Once this information has been extracted the vertical part of the solution is similar to the vertical launch.

Horizontal launch

In this case the only vertical motion is due to a downward acceleration. In this case we can set the downwards direction as the positive one. The initial vertical velocity in this case is 0 m/s.
How far away must the boat be for the ball to land in it when it is kicked horizontally off the 30 m cliff?
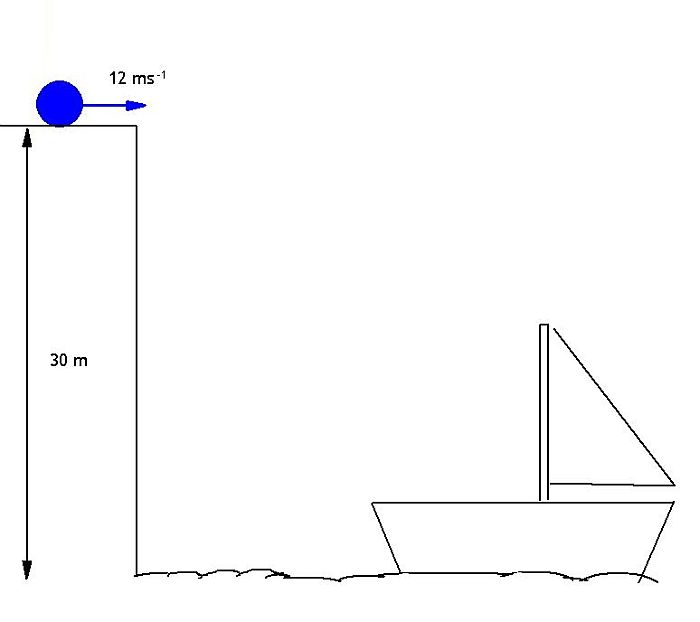
s_hor = ?
u_hor = 12 m/s
v_hor = 12 m/s
a_hor = 0 m/s²
t = ?
 
s_ver = 30 m
u_ver = 0 m/s
v_ver = ? m/s
a_ver = 9.8 m/s²
t = ?
In order to determine the time of the flight we need to use the vertical infromation first. Once we have this time we can apply it to the horizontal part of the flight, because it is a common time.
s = ut + ½at²
Since u = 0 m/s this simplifies to:
s = ½at²
30 m = ½ x 9.8 m/s² x t²
t = 2.47 s
t = 2.5 s
This time is how long it takes for the ball to reach sea level where the boat is. The horizontal velocity has remained at 12 m/s for this time, therefore we can now calculate how far away the boat is.
s = vt
s = 12 m/s x 2.47 s
s = 29.64 m
s = 30 m

Newton's Law of Universal Gravitation

The equation for Newton's Law of Universal Gravitation is: $$F=G\frac{m_1{m}_2}{r^2}$$
In this equation F = force due to gravitational attraction; m₁ and m₂ are the masses of the two objects; G is the gravitational constant; and r is the distance between the centres of the two objects.
The law is an example of an inverse square law. Doubling the distance between the objects reduces the gravitational force of attraction to ¼ of the original value. Three times the disance results in only 1/9 of the gravitational force of attraction. The force is inversely proportional to the distance between the two objects.
It also shows how that the force produced is proportional to the product of the masses.

Consider two people with masses of 75 kg and 63 kg. What is the force of gravitational attraction between these two people when they are 50 cm apart?
m₁ = 75 kg
m₂ = 63 kg
r = 50 cm = 0.5 m (remember to convert to SI units before substituting into the equation) $$F=G\frac{m_1{m}_2}{r^2}$$
F = 6.67 x 10^-11 m³ kg^-1 s^-2 x 75 kg x 63 kg/0.50² m²
F = 1.26 x 10^-6 N
F = 1.3 x 10^-6 N

Mass of a planet

An object of mass 5.0 kg experiences a force of 18.5 N on the surface of a planet. What is the mass of the planet, if it has a diameter of 6800 km?
F = 18.5 N
m₁ = 5.0 kg
m₂ = ?
r = 6800/2 km = 3400 km = 3400 x 10³ m = 3.4 x 10⁶ m (remember we have to use units, and the radius not the diameter)
G = 6.67 x 10^-11 m³ kg^-1 s^-2
18.5 = 6.67 x 10^-11 m³ kg^-1 s^-2 x 5.0 kg x m₂/(3.4 x 10⁶)² m²
m₂ = 6.41 x 10²³ kg
m₂ = 6.4 x 10²³ kg