Higher Physics

Special relativity

A simple primer on special relativity from physics.org which has been recorded on YouTube:

The great relativity show

Speed of Light

We start with the concept of inertial frames of reference. What is an inertial frame of reference?
Consider the following situation: I am standing on a platform watching a train pass by. The train is traveling in a straight line at a constant velocity. A scientist on the train throws a ball vertically just as I am passed. What is the path of the ball? To the scientist it is vertically up and down, as the ball returns to the scientist's hand. To me, the ball travels in a parabola, identical to projectile motion.

The two observers are in separate inertial frames of reference. A frame of reference that is not accelerating is an inertial frame. The obeservers in that frame, in the absence of external information appear at rest. Consider the room that you are in as you read this page. The room is not stationary, and therefore is an inertial frame of reference. The room is on our planet which is rotating on its own axis, while orbiting the sun, which is in turn orbiting in a spiral arm, the centre of our galaxy. Therefore the room is not actually stationary!
To think of an inertial frame just think of coordinate axes, x, y (and z if required). If the origin of the axis remains in a constant position with respect to you, you are in that inertial frame of reference.
In the second carraige you can see how the two different frames of reference would show the path of the ball.

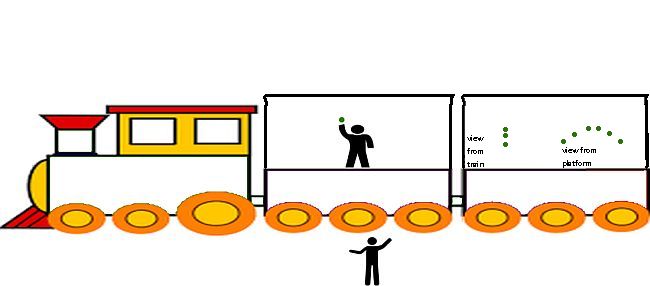
Let us now think about how fast the ball was travelling.

Train View	Platform View
Ball has a vertical velocity of 2 m/s as it is thrown.	Ball has a vertical velocity of 2 m/s and a horizontal velocity of 5 m/s from the movement of the train. This gives it a total velocity of 5.4 m/s at an angle of 22 degrees above horizontal

Notice that to the person on the platform the ball has an inital velocity that is greater than the observer on the train would measure.
Now let us replace the ball with a light beam and mirrors. A smiliar experiment will take place.

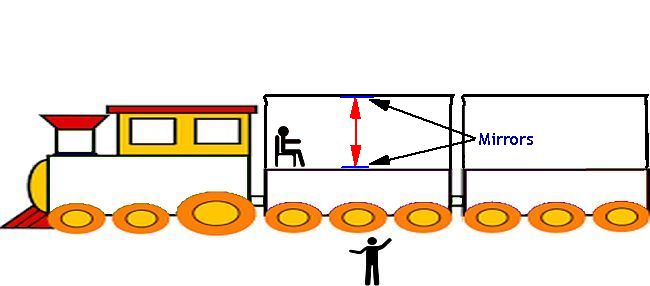
Let us look at the the train again, but this time we will represent the train view in the front carriage and the platform view in the rear carriage.

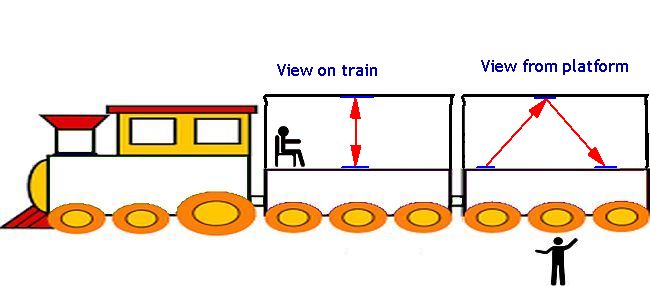
We can see that the distance travelled by the light in the front carraige is the height of the carraige. In the rear carraige, the view of a moving train from the platform shows that in the same time period that light has traveled a greater distance. What can we say about the spee of light for both observers? Is it different as was the case with the ball?
Einstein's special theory of relativity states that both viewers will measure light having the same speed. An essential part of the theory states that the speed of light is constant and that everyone in the universe, no matter how fast they are travelling in an inertial frame, would measure the speed of light as 3 x 10⁸ m/s. The speed of the inertial frame has no effect on the speed of light to any observer, either inside or outside the inertial frame. This is very different from classical physics.
The second essential component of the special theory of relativity is a simpler concept from the time of Gailileo which states:

any two observers moving at constant speed and direction with respect to one another will obtain the same results for all mechanical experiments

This leads to an important concept: velocity is NOT absolute
This concept is called Gallilean Invariance.
What this means is, if there is no external stimulus and we are moving at a constant velocity, then there is no knowledge of how fast we are moving. Remember the earth is orbiting the sun at around 30,000 m/s, so we are not static. In the lab/room it appears that we are not moving! All mecahnical measurements that we make appear to function as if we are in a non-moving environment.
Due to our distance from the sun we are approximating our motion as in a straight line in the timeframe that we take to make laboratory measurements!
Einstein worked on electromagnetic radiation, which according to Maxwell's equations travelled at a value, c, which we call the speed of light. He realised that in order to reconcile the Galilean principles with the fixed value of the speed of light, he would have to introduce some transformations. Based on the work of Lorentz in 1904.
This led to some bizzare consequences, maintaining the speed of light at a constant value for all inertial frames of reference, even for those looking into faster or slower moving frames of reference.

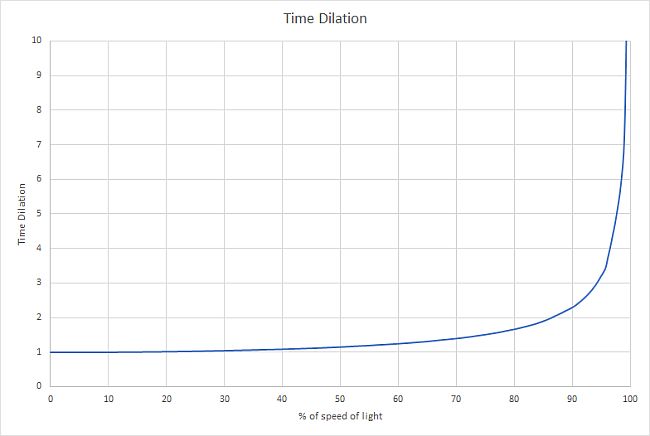
Time dilation

One of the most startling consequences of special relativity is that any moving clock slows down relative to a stationary observer. At speeds much slower than the speed of light this effect is very small, but as we get closer to the speed of light it becomes increasingly greater. Looking at the graph below shows how time dilation changes as you approach the speed of light.

The equation for time dilation is:

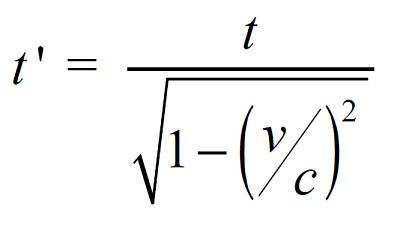
Where
t' change in time
t is the time in the rest frame
v is the relative velocity of the frame
c is the speed of light

Consider a spaceship in the future travelling at 0.9c. How slow would its clock be compared to a clock here on earth?

$$\mathrm{t\prime }=\frac{t}{\sqrt{1-<!--\; ?\; -->(\frac{v}{c}{)}^2}}$$ $$t\prime =\frac{1}{\sqrt{1-<!--\; ?\; -->(\frac{\mathrm{270000000}}{\mathrm{30000000}}{)}^2}}$$

On solving this, 1 second on earth appears to be 2.3 times slower on the spaceship. In other words, when 1 second has passed on the rocket from our earth perspective, 2.3 seconds will have passed here on earth!

Length contraction

Since time is no longer an absolute measure, let us also consider what happens to the length of objects as we approach the speed of light. Remember that speed is given by distance/time. We have just seen that time changes as we approach the speed of light. Since the speed of light does not change, there must also be a change to the distance measurement as well. The lenght of any object will appear shortened in the direction of motion.
If we consider an object that we can see at rest with a length of 100 m. Let us see how its length changes as it passes us at increasing speeds. Note the wingspan of the plane is 20 m.

At rest: Banner = 100 m, Wingspan = 20 m

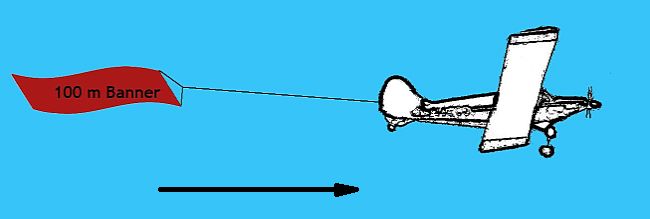
At 10% of the speed of light: Banner = 99.5 m, Wingspan = 20 m

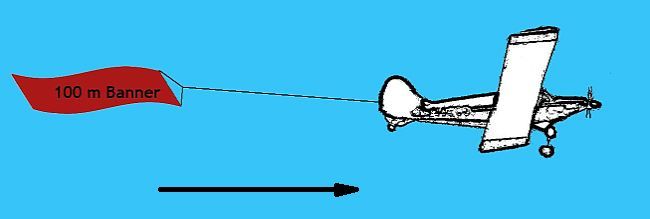
At 86.5% of the speed of light: Banner = 50 m, Wingspan = 20 m

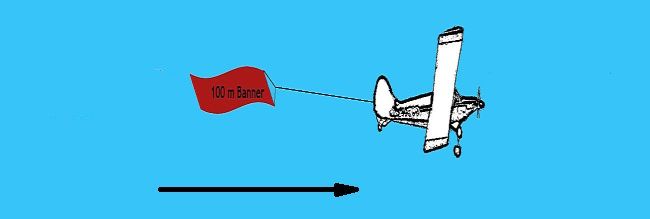
At 99% of the speed of light: Banner = 14 m, Wingspan = 20 m

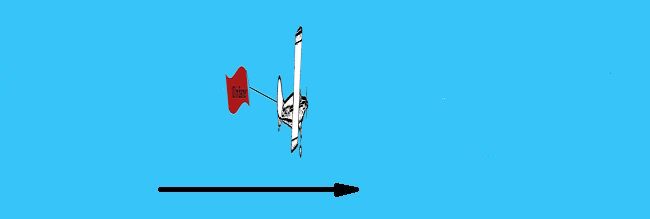
At 99.9% of the speed of light: Banner = 1.5 m, Wingspan = 20 m

As you can see, the only dimension that is changed is the one in the direction of motion. The wingspan remains at 20 m throughout all the of the examples.
The equation that allows us to calculate the change in length is;

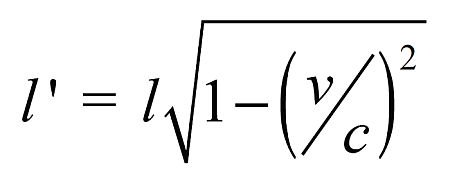
Where
l' change in length
l is the length in the rest frame
v is the relative velocity of the frame
c is the speed of light

A particle is traveling through the Earth's atmosphere at a speed of 0.75c. An observer on earth measures it traveling a distance of 2.50 km. How far does the particle travel in the particle's frame of reference? $$\mathrm{l\prime }=l\sqrt{1-<!--\; ?\; -->(\frac{v}{c}{)}^2}$$ $$l\prime =\mathrm{2.50\; km}\sqrt{1-<!--\; ?\; -->(\frac{\mathrm{0.75c}}{c}{)}^2}$$ $$l\prime =\mathrm{1.65\; km}$$

Muon Evidence

Muons are short-lived sub-atomic particles that enter the earth's atmosphere at a height of about 10 km when the atmosphere interacts with cosmic rays. They pass through the atmosphere at 0.995c when observed from the earth.
Muons have a half-life of 2.2 x 10^-6s in their frame of reference. In their frame of reference the average distance travelled is 660 m. This means that we should not detect many muons down on the surface, but experimental detection has shown that many do arrive on the surface of the earth. Due to their high speeds we have to look at relativistic effects.
How far in the muon's frame of reference does it travel compared to the earth frame of reference of 10 km?

$$\mathrm{l\prime }=l\sqrt{1-<!--\; ?\; -->(\frac{v}{c}{)}^2}$$ $$l\prime =\mathrm{10\; km}\sqrt{1-<!--\; ?\; -->(\frac{\mathrm{0.995c}}{c}{)}^2}$$ $$l\prime =\mathrm{100\; m}$$

From this we can see that there will be many muons which will reach the the surface of the earth.

When a muon decays, because it ie heavier than an electron, but is one of the lepton family,it decays into an electron. The other products of this process produced are two neutrinos, which satisfy conservation laws for leptons.