Laws of Thermodynamics

The zeroth law of thermodynamics states that if two thermodynamic systems are each in thermal equilibrium with a third one, then they are in thermal equilibrium with each other.

The First Law of Thermodynamics states that energy cannot be created or destroyed, but it can be transferred from one location to another and converted to and from other forms of energy. This is well known as the law of conservation of energy.

The second law of thermodynamics says that when energy changes from one form to another form, or matter moves freely, entropy (disorder) in a closed system increases. One result of the second law is that heat energy spontaneously flows from a region of higher temperature to one of lower temperature. This process can be reversed with work being done on the system, such as air conditioning units.

Temperature

Temperature is a measure of how hot or cold something is. It is a measure of the average kinetic energy of the particles for which the temperature is taken. Greater avereage kineitc energy means that the substance is at a higher temperature than that with lower average kinetic energy.

Temperatures are also measured in scales. Three scales that occur most frequently are:

1. Kelvin
2. Celsius
3. Fahrenheit

When working with temperature in physics if there is a temperature change then working in Celsius and Kelvin will both give meaningful results. If it is the individual temperature that is required then you MUST use Kelvin

To convert to Kelvin from Celsius use the following relationship:

$$\mathrm{T\; (K)}=\mathrm{T\; (°C) + 273}$$

---

Converting centigrade to kelvin

Attempt to solve the question yourself before clicking the solve button!

An object has a temperature of °C. Calculate the temperature of the object in kelvin.

---

Temperature and Kinetic Energy

The temperature of any object is related to the average kinetic energy of the particles making up the object. When the temperature is increased then the average kinetic energy of the particles must also increase.

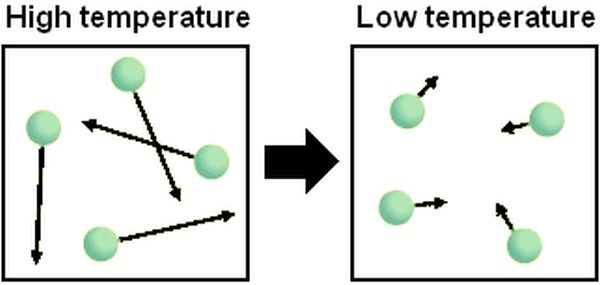
Note the longer arrows showing that the matter particles are moving faster on average at a higher temperature.

Specific Heat Capacity

A simple question to ask about the difference between heat energy and temperature is to ask about the temperature of a lit match and a bath tub full of warm water.

Clearly the match has the higher temperature.
The subsequent question to ask is about which one contains more heat energy? People clearly understand that it takes more than the amount of heat energy in a single match to warm the water in the bath and so will indicate that the bath water contains more energy. There may be a lower temperature in the bath water, but because there is so much water, there is a much greater heat energy content.

It is clear from the above example that heat energy and temperature are not the same thing. They are related, but in physics it is important to recognise their difference.

The equation connecting heat and temperature takes into account the need to know how much material there is, and what the material is made from. It is given in the equation below:

$$E_h=\mathrm{cm\Delta T}$$

where
E_h is heat energy
c is the specific heat capacity of the material
m is the mass of the material
ΔT is the change in temperature (either in °C or K)

Specific heat capacity is defined as the amount of heat energy required to increase 1 kg of the material by 1 °C. Please note that in physics the unit of mass is the kilogram, and this differs from chemistry where the unit of mass is the gramme. Therefore the values used are the same numbers, but 1000 times bigger in physics. It is a common mistake of students at Nat 5 to confuse the numbers. Below is a tbale of common values, which is given in the data sheet in the exam. The values in the data sheet may change because of the materials in the question paper, so this is not a definitive table.

Material	Specific heat capacity in J kg-1 °C-1
Alcohol	2350
Aluminium	902
Copper	386
Glass	500
Ice	2100
Iron	480
Lead	128
Oil	2130
Water	4180

Experiment to determine the SHC of a metal

It is possible to determine the specific heat capacity of a metal by supplying a known amount of energy to a known mass of metal and determining the tepmerature change of the metal. For ease of calculation we will use a 1.0 kg block of aluminium, a thermometer, insulation, an electric heater attached to a Joulemeter. If a Joulemeter is not available then the current and voltage can be monitored over time to know the electrical power of the system. This can be converted to electrical energy using:

$$P=\mathrm{IV}$$

and

$$P=\frac{E}{t}$$

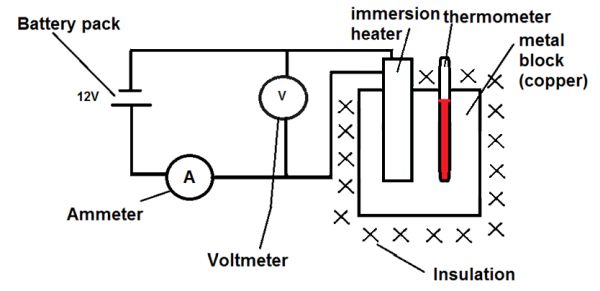
This experiment relies upon the fact that energy cannot be created or destroyed, only converted from one form to another. In this experiment we are using electrical energy and converting it into heat energy.
In an experiment that took 10 minutes (600 seconds) the average current in the circuit was 2.5 Amps. The average voltage was 8.6 V. This resulted in a temperature change from 23.0 °C to 36.5 °C with a 1.00 kg block of aluminium.
Let us start by calculating the average power of the circuit.
I = 2.5 A
V = 8.6 V

$$P=\mathrm{IV}P=\mathrm{2.5 \times 8.6}P=\mathrm{21.5\; W}$$

The total energy supplied can be calculated from:

$$P=\frac{E}{t}\mathrm{21.5}=\frac{E}{\mathrm{600}}E=\mathrm{12900\; J}$$

Using the energy supplied, the mass of 1.00 kg and the temperature change we can work out the specific heat capacity of aluminium.

$$E_h=\mathrm{cm\Delta T}\mathrm{12900}=\mathrm{c \times 1.00 \times (36.5 - 23.0)}c={\mathrm{956\; J\; kg}}^{\mathrm{-1}}{\mathrm{ s}}^{\mathrm{-1}}$$

The value in the table above is 902 J kg^-1 s^-1 which is quite close to the experimental value of 956 J kg^-1 s^-1. The main reason for the difference in values will be heat loss to the surroundings, which will result in a lower temperature rise than expected. Some energy will also have been lost to the resistance in the circuit, but this will be very small in comparison to the heat loss to the surroundings.

In exam board questions the insulation is often omitted and students are asked how to improve the experiment. In this case adding insulation to reduce heat loss to the surroundings will gain marks. If there is already insulation then improving the experimental results can be carried out by reducing the time of heating. |This reduces the heat loss to the surroundings, but it also results in a lower temperature change.

Example 1

10 g of ice is heated from -4 °C to 0 °C. How much heat energy was supplied to the ice?
m = 10 g = 10 × 10^-3 = 0.010 kg
ΔT = 0 − (-4) = 4 °C
c = 2100 J kg^-1 s^-1 (from the table above - note that this is different from the specific heat capacity of water!)

$$E_h=\mathrm{cm\Delta T}{E}_h=\mathrm{2100 \times 0.010 \times 4}{E}_h=\mathrm{84\; J}$$

---

Determining the energy used to heat some water

Attempt to solve the question yourself before clicking the solve button!

A bath filled with kg of water. The initial temperature of the water is °C and the final temperature of the water is °C. Calculate the energy required to heat the water.

---

Example 2

What would be the temperature of water be when 250 g of water cools from 65 °C giving out 47 kJ of energy?
E_h = 47 kJ = 47 x 10³ J
c = 4180 J kg^-1 s^-1
m = 250 g = 0.250 kg
ΔT = ?

$$E_h=\mathrm{cm\Delta T}\mathrm{47000}=\mathrm{4180 \times 0.250 \times \Delta T}\mathrm{\Delta T}=\mathrm{45\; °C}$$

Since the change in water temperature is 45 °C, the new temperature will be (65 - 45) = 20 °C.

---

What is the temperature change?

Attempt to solve the question yourself before clicking the solve button!

A heated swimming pool transfers kJ of energy to the surroundings. The initial temperature of the water is °C. The pool is filled with kg of water. Calculate the final temperature of the water.

---