Specific Latent Heat

When boiling a beaker of water the temperature of the water does not increase. A typical graph for heating water at a constant rate looks like the one below:

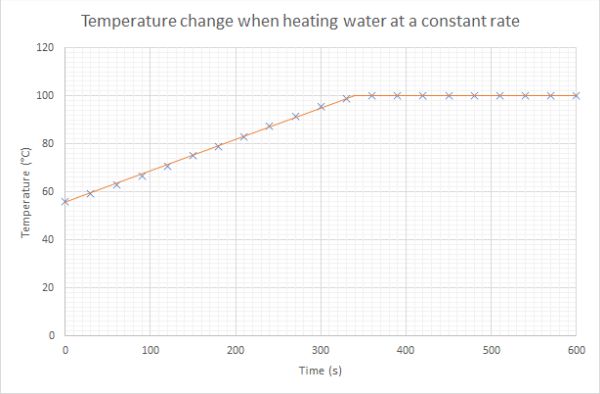
Since there is a constant supply of heat energy where does the energy go when water is boiling? We cannot create or destroy energy, so the additional heat energy added must be going somewhere.

The added heat energy is going in to the changing of state from liquid to gas. The average kinetic energy of the particles is staying the same because the temperature is not changing. Instead it is going in to breaking the forces holding the particles together as a liquid. Because this energy is being stored in the gas it is a type of potential energy. When the gas goes back to being a liquid this potential energy will be released to the surroundings.

In the case of a liquid forming a gas or vice versa we call this the latent heat of vaporisation.

In the case of a solid forming a liquid or vice versa we call this the latent heat of fusion.

Graph of change of state

In the graph below it is possible to identify where the changes of state are taking place because the graph levels out at the melting point, and also at the boiling point.

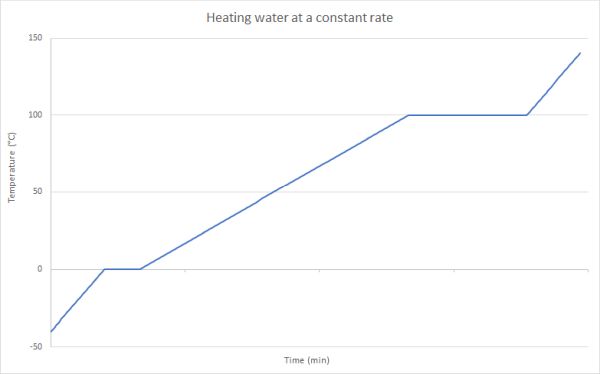
In the graph above you can see that at the melting point of ice (0 °C) and the boiling point of water (100 °C) that the graph is horizontal. It remains horizontal until the state change is complete. Once the state change is complete the heat energy being added can continue to increase the temperature of the water in its new state which is shown by the temperature increasing.

Looking at the graph you may also notice that the rate of temperature increase for both ice and steam is higher than for liquid water. This is because the specific heat capacity of ice and steam are both around 2000 J kg^-1 °C^-1, while the value for liquid water is 4180 J kg^-1 °C^-1, indicating it takes twice the energy to produce the same temperature change.

Specific Latent Heat Calculations

To be able to calculate the amount of heat energy involved in a change of state experiment it is important to know that the relationship between heat energy and mass of material is given by:

$$E_h=\mathrm{ml}$$

Where:
E_h is the heat energy change
m is the mass of the material
l is the latent heat of the material

In the National 5 data sheet tables of latent heats of vaporisation and latent heats of fusion can be found. Below are example tables, but please remember that these are not fixed, and the data in the tables may change depending on questions in the exam paper.

Latent Heat of Fusion

Material	Specific latent heat of fusion in J kg-1
Alcohol	0.99 x 105
Aluminium	3.95 x 105
Carbon dioxide	1.80 x 105
Copper	2.05 x 105
Iron	2.67 x 105
Lead	0.25 x 105
Water	3.34 x 105

Latent Heat of Vaporisation

Material	Specific latent heat of vaporisation in J kg-1
Alcohol	11.2 x 105
Carbon dioxide	3.77 x 105
Glycerol	8.30 x 105
Turpentine	2.90 x 105
Water	22.6 x 105

We can use the data in the tables above to work out the heat energy required to change a specific mass of material at its melting point, or at its boiling point.

Example 1

How much heat energy is required to turn 5.0 kg of lead into molten lead at its melting point of 328 °C?

E_h = ?
m = 5.0 kg
l = 0.25 x 10⁵ J kg^-1

$$E_h=\mathrm{ml}{E}_h={\mathrm{5.0\; \times \; 0.25\; \times \; 10}}^5{E}_h={\mathrm{1.25\; \times \; 10}}^5{\mathrm{ J\; kg}}^{\mathrm{-1}}$$

Example 2

What mass of water is converted to steam when 100 kJ of energy is added to water at its boiling point of 100 °C?

E_h = 100 kJ = 100,000 J
m = ? kg
l = 22.6 x 10⁵ J kg^-1

$$E_h=\mathrm{ml}{\mathrm{1.0\; x\; 10}}^5={\mathrm{m\; \times \; 22.6\; \times \; 10}}^{5}m=\mathrm{0.044 kg}$$

Note that for 100 kJ of energy only 44 g of water is converted to steam at 100 °C. The latent heat of vaporisation of water is very high.

---

What mass has been converted to gas

Attempt to solve the question yourself before clicking the solve button!

Determine the mass of iron at its melting point that is converted to molten iron when kJ of energy is supplied. The latent heat of fusion of iron is 2.67 x 10⁵ J kg^-1.

---

Example 3

In more complex examples the SQA may combine both specific heat capacity and latent heat questions. This example is of a combined type fo question

How much energy is required to convert 10 g of ice at -4.0 °C to water at 20 °C?

In order to calculate this we need to break the calculation into three parts
a) the heat energy required to bring 10 g of ice at -4.0 °C to 0 °C
b) the heat energy required to melt 10 g of ice at 0 °C
c) the heat energy required to raise 10 g of water from 0 °C to 20 °C

a)
E_h = ?
m = 10 g = 0.010 kg
c = 2100 J kg^-1 s^-1 (from SHC table in Specific Heat Capacity)
ΔT = (0 - (-4.0)) = 4.0 °C

$$E_h=\mathrm{cm\Delta T}{E}_h=\mathrm{2100\; \times \; 0.010\; \times \; 4.0}{E}_h=\mathrm{84\; J}$$

b)
E_h = ?
m = 10 g = 0.010 kg
l = 3.34 x 10⁵ J kg^-1 $$E_h=\mathrm{ml}{E}_h={\mathrm{0.010\; \times \; 3.34\; \times \; 10}}^5{E}_h={\mathrm{3.34\; \times \; 10}}^3\mathrm{ J}$$

c)
E_h = ?
m = 10 g = 0.010 kg
c = 4180 J kg^-1 s^-1 (from SHC table in Specific Heat Capacity)
ΔT = (20 - 0) = 20 °C

$$E_h=\mathrm{cm\Delta T}{E}_h=\mathrm{4180\; \times \; 0.010\; \times \; 20}{E}_h=\mathrm{840\; J}$$

The total heat energy required is the addition of the answers to a), b) and c)

E_h = 84 + 3340 + 840 = 4260 J

---

What mass has been converted to gas

Attempt to solve the question yourself before clicking the solve button!

Water at a temperature of °C is brought to the boil and further heated to °C as a gas. Calculate the amount of energy supplied to convert g of water at the initial temperature to steam of the final temperature.

The specific heat capacity of water is 4180 J kg^-1 °C^-1
The specific heat capacity of steam is 2010 J kg^-1 °C^-1
The latent heat of vaporisation of water is 22.6 x 10⁵ J kg^-1

---