National 5 Physics

Energy

What is energy? The late Richard Feynman, one of the most important physicists of the 20^th Century can be quoted here:

It is important to realize that in physics today, we have no knowledge of what energy is.¹

This is still true today. We know of lots of different kinds of energy, but we do not really know what energy is. We can see the effects of energy, and can measure it in its many different forms, but cannot tell what it is. One of the key facts that we have learnt in all of the studies of energy is that it can be transformed from one kind to another, but it cannot be created or destroyed.

Conservation of energy
Energy cannot be created or destroyed, it can only be converted from one form to another in a closed system. If there is any additional energy it must have come from somewhere outside the system beng studied. If there is too little energy then some must have been lost to outside the system because this law has so far never been broken.

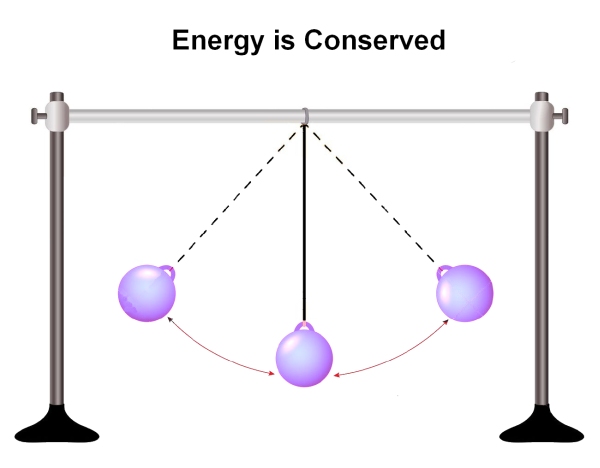
The pendulum above converts gravitational potential energy into kinetic energy and back to gravitational potential energy. The point of maximum gravitational potential energy is at the top of each swing. The point of maximum kinetic energy is at the bottom of the swing. If there was no friction in the system the pendulum would continue swinging forever.

Example

What energy transformations occur in the following system. You eat breakfast, then walk over to a friend's house. On the way you switch a torch on because it is dark in the winter and the street lights are not working. You slip and fall down a small hill, which you then have to walk up again.

When you eat food you are storing chemical energy, which you convert to heat and kinetic energy when you move. In the torch the batteries also store chemical energy. This is converted to light and heat when the torch is switched on. When you slip gravitational potential energy is converted to kinetic energy. When you walk back up the hill you convert chemical energy into kinetic energy and stored gravitational potential energy.

Work

The word work is used widely every day and generally means to do some form of activity, physical or mental that produces or services something. In physics the technical word 'work' has a very specific meaning and so it is important to realise that when using this word in physics we must learn and understand its definition.
In physics work is defined as the product of the amount of force applied to an object, and the distance that object has moved in the direction of the force. The equation showing this relationship can be written in one of two ways:

$E_W=\mathrm{Fd}$
or
$W=\mathrm{Fd}$

Think of a book being moved across a level table by an average force of 10 N, and that it was moved 15 m by that average force. How much work has been done on the book to move it across the table?

$E_W=\mathrm{Fd}$
$E_W=\mathrm{10\; \times \; 15}$
$E_W=\mathrm{150\; J}$

If we were then to be asked how much work was done against the gravitational field in the book moving example we would have to look at how different the height of the book was at the end, compared to the beginning. In this case, since the table is level, the book is at the same height. Therefore the distance moved vertically is 0 m. Since anything multiplied by 0 is 0, there is 0 J of work done against the gravitational field in this example.

Gravitational Potential Energy

Gravitational Potential Energy (GPE) is the energy an object has gained when raised above the surface of the Earth. Work has to be done on the object to raise it, and this is stored as gravitational potential energy, which can be released when the object is lowered. This is how hydroelectric systems work. Water is raised to a high resevoir - giving it gravitational potential energy (when it rains this work is done for free!). When the water runs down the hill in a pipe the gain in kinetic energy from the conversion of GPE can then be used to drive a turbine as the water moves past. Some of the kinetic energy the water has gained is then converted to electrical energy by the generator through the movement in the turbine.

The equation linking height, mass and the stored GPE is given below:

$$E_p=\mathrm{mgh}$$

Notice that this is an energy equation with the final answer having a vlaue in Joules/

Example

How much energy is transferred from the crane to the 50 kg crate which is raised 8 m from the deck of a ship?

E = ?
m = 50 kg
h = 8 m
g = 9.8 m/s²

$$E_p=\mathrm{mgh}$$ $$E_p=\mathrm{5o \times 9.8 \times 8}$$ $$E_p=\mathrm{3920\; J}=\mathrm{3.9\; kJ}$$

Gravitational potential energy is defined as the energy an object posesses due to its poistion in a gravitational field.

Kinetic Energy

When an object is moving it has kinetic energy. This is the energy of motion. It depends on both the mass of the object and how fast it is travelling. The relationship is expressed as follows:

$$E_k=\frac{1}{2}{\mathrm{mv}}^2$$

Example

A truck with a mass of 1500 kg is travelling at 2 m/s. How much kinetic energy does the truck have?

E = ?
m = 1500 kg
v = 2 m/s

$$E_k=\frac{1}{2}{\mathrm{mv}}^2$$ $$E_k=\frac{1}{2}{\mathrm{\times 1500 \times 2}}^2$$ $$E_k=\mathrm{3000\; J}=\mathrm{3.0\; kJ}$$

Often in physics we may be given information about one kind of energy and be expected to remember the concept of the conservation of energy to derive another type of information from the system. We should know that it is not possible to create or destroy energy. It is only possible to convert it from one form to another.

Example

A box with a mass of 25kg has 2.0 kJ of gravitational potential energy.The box falls and all the GPE is converted to kinetic energy. How fast is the box moving due to the conversion of GPE into kinetic energy>

$$E_k=E_p$$ $$E_p=E_k=\frac{1}{2}{\mathrm{mv}}^2$$ $${\mathrm{2.0 \times 10}}^3=\frac{1}{2}{\mathrm{ \times 25 \times v}}^2$$ $$v=\mathrm{12.6\; m/s}=\mathrm{13\; m/s}$$

Example

Just before touchdown, small engines fire on the bottom of the Module (shown below), slowing it down further. The work done by the engines is 8.0 × 10⁴ J over a distance of 5.0 m.

Calculate the force produced by the engines.

F = ?
E = 8.0 × 10⁴ J
d = 5.0 m

$E_W=\mathrm{Fd}$
so
${\mathrm{8.0 \times 10}}^4=\mathrm{F \times 5.0}$

F = 16,000 N

The module with astronauts has a mass of 400 kg. How much slower did the small engines make the module?

v = ?
m = 400 kg
E_e = E_k = 8.0 × 10⁴ J

$$E_k=\frac{1}{2}{\mathrm{mv}}^2$$ $${\mathrm{8.0 \times 10}}^4=\frac{1}{2}{\mathrm{ \times 400 \times v}}^2$$

v = 20 m/s
The module has been slowed by 20 m/s.

---

Work Done - How much force?

Attempt to solve the question yourself before clicking the solve button!

Just before touchdown the Falcon 9 rockets fire expending kJ of energy against gravity. It travels for m while doing this work. Calculate the force is being produced by the engine?

---

Work Done - How far?

Attempt to solve the question yourself before clicking the solve button!

Just before touchdown the Viking 2 Mars probe rocket fired expending kJ of energy against gravity. The force generated by the engines was N while doing this work. What distance did the Viking probe travel during this time?

---

How fast is it moving?

Attempt to solve the question yourself before clicking the solve button!

A box with a mass of kg is raised by a crane from the ground. The height the baox was raised to was m
(a) Calculate the potential energy gained by the box.
(b) If the cable was to break when the box was at this height determine the speed would it have just before hitting the ground (ignore air resistance).

---

How high was the ball?

Attempt to solve the question yourself before clicking the solve button!

A ball with a mass of kg hits the ground with a vertical velocity of m s^-1. The ball was dropped vertically from a stationary start
(a) Calculate the kinetic energy of the ball.
(b) Determine the vertical height the ball was dropped from (ignore air resistance).

---