National 5 Physics

Newton's Laws

Isaac Newton was a key scientist in the scientific revolution in the late 1600s and early 1700s. His contributions to mathematics, physics, astronomy helped pave the way for much of modern mechanics, optics and cosmology. In this section we will concentrate on his contribution to the field of mechanics.

Forces

What is a force? A force is something that can have an effect on an object. Generally you cannot see a force, but you can see its effect on an object. An example is the force of gravity, which causes an object to accelerate to the ground when dropped. When there is an unbalanced force it will result in one or more of three consequences:

1. Change of velocity
2. Change of direction
3. Change of shape

There are two principal types of force:

1. Contact force - push, pull, friction etc
2. Non-contact force - magnetic, electric and gravitational.

Force Fields

When considering non-contact forces physicists have developed the concept of a field. A field is defined as the region of space where the effects of a non-contact force can be detected. One of the most common fields we are familiar with is the gravitational field here at the surface of the Earth. When we were babies the natural scientist in us checked to see if things always fell down. Our experiments involved dropping things, pushing things of the high chair or table, and the results were always the same. Whatever the object it always fell down. We cannot see the force that is causing this, but we can see its effect. Therefore the act of dropping something shows us the presence of the gavitational field, which accelerates objects at 9.8 m s^-2 to the ground.

Newton's Laws of Motion

The first law of motion is that an object will continue to stay at rest, or move with a constant velocity in the absence of an unbalanced force.

The second law of motion is that the acceleration of an object is directly proportional to the force applied in the same direction as the force and inversely proprotional to the mass of the object.
The equation for this law is simply:

$$F=\mathrm{ma}$$

The third law of motion states that for every action force there is an equal ond opposite reaction force.

The First Law of Motion

This is the law of balanced forces. Where there is no change of speed, change of direction or change of shape all the forces acting on an object must be balanced. The motion of the object will be one of two possibilities
a) at rest, not moving
b) moving in a straight line at a constant speed.

Newton imagined an ideal world where there was no friction opposing the direction of motion. In this situation the object that was subject to balanced forces would continue to move in a straight line at a constant speed forever. This does happen to objects in deep space, because there is no friction in a vaccuum.

Here on Earth we always have friction, and so the system is not ideal. In exam questions it may state that friction or air resistance can be ignored. In this case the question is asking for a response to an ideal situation with no change of speed, direction or shape when dealing with balanced forces. It is important to note that often students incorrectly think that balance forces means that the object is not moving. This is only true if the abject was already at rest. If the object was in motion, then it will continue moving in a straight line at a constant speed until acted upon by another force. Balanced forces requires no acceleration, but the object can be moving already. Consider an object dropped from a great height that is at terminal velocity. The forces on the object are balanced (weight pulling down and air resistance pushing up) an the object is moving with a constant speed. It is certainly not stationary! This is an example of Newton's First Law of Motion.

Example

A block of mass 3.0 kg is pulled across the bench with a 6 N force. The block travels with a constant velocity.

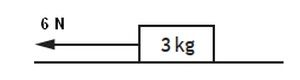
How great is the friction force acting on the block?

Since there is no acceleration - the block is moving with a constant velocity - the forces on the block must be balanced. Therefore the friction force opposing the pulling force must have the same size to balance the forces. The size of the friction forcce is therefore 6 N. The direction it operates in is against the direction the block is moving in.

The Second Law of Motion

The second law makes it clear that when there is an unbalanced force acting on an object that can move, it will produce an acceleration. Ths size of the acceleration is directly proportional to the size of the unbalnaced force. The greater the mass of the object, the smaller the acceleration of the object. Experimentally it can be shown that the acceleration is inversely proportional to the mass. The relationship that expresses this is:

$$F=\mathrm{ma}$$

Example

What is the acceleration of a car and driver with a combined mass of 1200 kg when two forces are acting upon it. The engine force is 650 N and the friction force is 50 N.

The forces are acting in opposite direction to each other so to work out the size of the unbalanced force we must subtract the friction force from the engine force.
F_un = Engine force − Friction force = 650 N − 50 N = 600 N
F_un = ma
600 = 1200 × a
a = 0.5 m s^-2

---

Acceleration calculation

Try and solve the question before clicking the solve button to check your answer

The engine force of a car is N. The mass of the car is kg. The firction force opposing the engine force is shown to be N. Calculate the acceleration of the car.
(This routine is only setup for integers. Using numbers with decimal points may result in rounding errors.)

---

Forces at right angles

Along with adding forces in the same or opposite directions you will need to be able to add forces acting at right angles.

Example

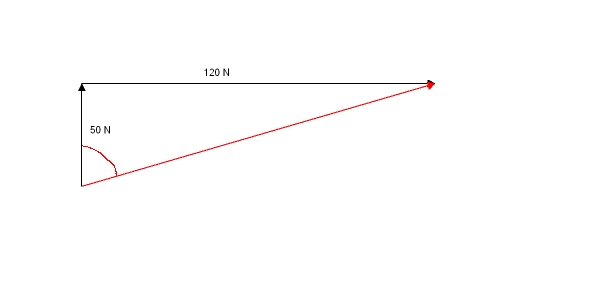
Two forces are acting on a box as illustrated in the diagram below:

What is the magnitude of the resultant force, and at which angle is the force directed?

There are two ways to solve this problem.

• Scale Diagram

When drawing a scale diagram there are key points to remember.

1. Write down the scale selected
2. Add the arrows head to tail
3. Watch for diagrams where the arrows are tail to tail or head to head. These need to be redrawn to comply with rule 2 above
4. Use a ruler and measure accurately
5. A set square can help with making sure that the forces are at 90° to each other
6. All angles should be measured with a protractor.
7. Use a sharp pencil of all lines
8. Draw arrow heads on the vectors in the appropriate directions

In the above diagram of the box a suitable scale would be 1 cm = 10 N. This would end up with a right angle triangle where the sides were 5 cm vertical and 12 cm to the right

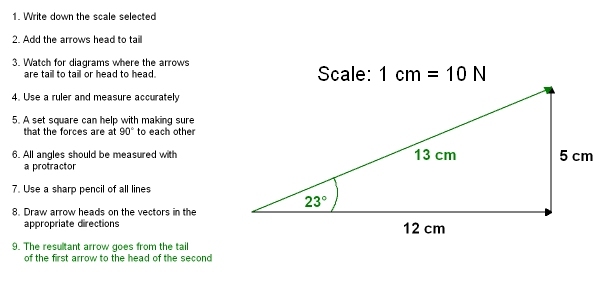
The result of this scale drawing can be seen with a vector of 13 cm length acting at 23° above horizontal to the right. This means that the resultant force has a magnitude of 130 N at an angle of 23° above the horizontal to the right.

• Use Pythagoras and trigonometry

First sketch a diagram to show the vectors being added to ensure that you are adding them head to tail. You will see from the box diagram above that the vectors are tail to tail in the diagram. The sketch diagram does not need to be measured.

To determine the size of the resultant force we must use Pythagoras:

Pythagorean theorem

$c^2=a^2+b^2$
$c^2={\mathrm{50}}^2+{\mathrm{120}}^2$
$c=\sqrt{\mathrm{16900}}$
$c=\mathrm{130\; N}$

To determine the angle we can see that:

$\mathrm{tan(\theta )}=\frac{\mathrm{120}}{\mathrm{50}}$
$\theta =\mathrm{67°}$

From this we can see that the answer is the same as the one determined by the scale drawing. Remember that 67° from vertical is 90 − 67 = 23° above horizontal to the right. We would have expected both answers to be the same. You can also see that it does not matter which force gets moved from tail to tail, just as long as the two forces are added head to tail.

---

Resolving perpendicular forces

Attempt to solve the question yourself before clicking the solve button!

A box is pushed horizontally with a force of N. A vertical force of N acts at right angles to the direction of the horizontal push. Determine the resutlant force acting on the box

---

Swimming Example

Attempt to solve the question yourself before clicking the solve button!

A swimmer is swimming directly across a river. The speed of the swimmer is m s^-1. The current of the river acts at right angles to the swimmer and the actual speed of the swimmer is m s^-1. Determine the speed of the river's current acting on the swimmer.

---

Weight

The term weight is used widely in everyday life, and most people refer to the weight of an object in kilogrammes. In physics the definition of weight is more precise than used in everyday language. Weight depends on the strength of the gravitational field (which produces an acceleration) and the mass of the object. This means that weight is a force because it depends on acceleration and mass just like the expression for Newton's 2^nd Law. Instead of using F = ma we use the following relationship instead.

$$W=\mathrm{mg}$$ Where
W = weight (N)
m = mass of the object (kg)
g = gravitational field strength (either N/kg or m s^-2

The mass of the object is a measure of how much matter there is present in the object. It is the same at all points in the universe because the amount of matter in the object does not change.

The weight of a 10 kg object will depend where in space the object is. If it is in deep space it will have a weight of 0 N, because there is no gravitational force attracting it.
W = mg = 10 ×0 = 0 N
If it is here on planet Earth, the acceleration is 9.8 m s^-2. Therefore the 10 kg object has a weight of:
W = mg = 10 ×9.8 = 98 N.
If it is on the moon, the acceleration is 1.6 m s^-2. Therefore the 10 kg object has a weight of:
W = mg = 10 ×1.6 = 16 N.

Example

What is the gravitational field strength on Mars if the 10 kg object has a weight of 37 Newtons?

$$W=\mathrm{mg}$$ $$\mathrm{37}=\mathrm{10 \times g}$$ $$g={\mathrm{3.7\; m\; s}}^{\mathrm{-2}}$$

Example

A student in class states that if they moved to Mars their weight of 66 kg on Earth would only be about a third of this on Mars because its gravitational field strength is about one third of the value here on Earth. They claim that their weight would be approximtely 22 kg. Using your knowledge of physics explain whether this is true or false.

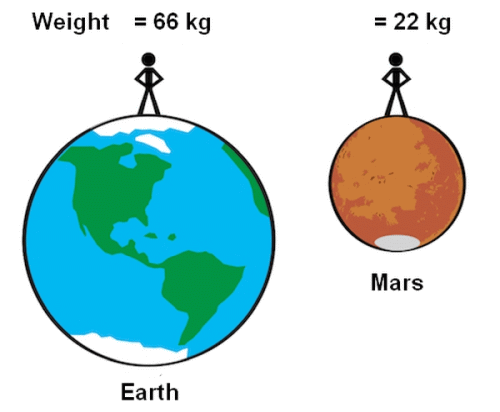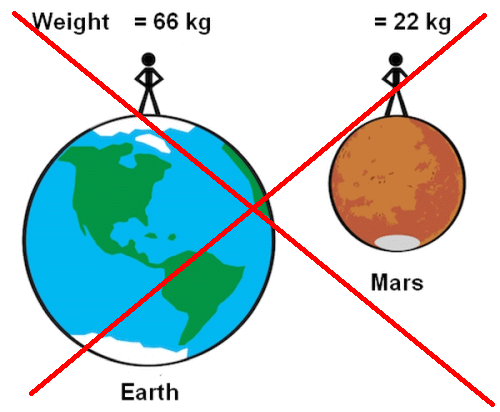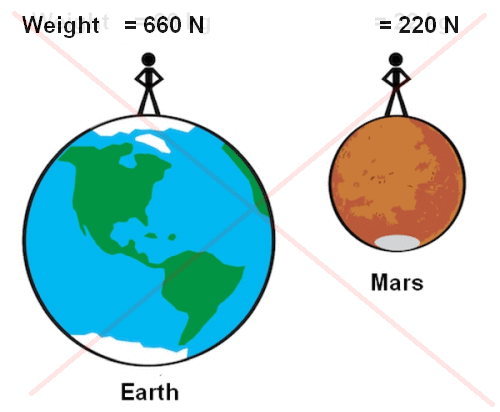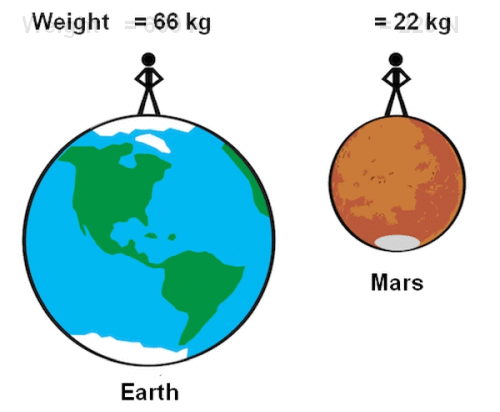
In this example we should note the confusion in the use of language by the student. Weight is a force, and all forces are measured in Newtons, NOT kilogrammes! The weight of the student on earth is approximately 660 N since the value of g ≈ 10 N/kg. The weight of the student on Mars would be approximately 220 N since the value of the gravitational field strength is about 1/3 the value of g on Earth. Weight is calculated using the equation, W = mg. The student's mass does not change because it is the same at all points in the universe and only depends upon the amount of matter present.

The Third Law of Motion

Think of a book resting on a table. It is not moving. Newton's First Law states that all the forces acting upon it must be balanced because it is at rest. We know that the force of gravity is acting on the book, because it is sitting on the desk. What is the equal and opposite force acting on the book to balance the gravitational force pulling the book to the centre of the Earth?

In the diagram below we can see that the downward arrow represents the weight of the book. What does the upward arrow represent. This upward arrow is the same length and therefore the same size as the weight force, but it acts in the opposite direction. The upward force is called the normal reaction force.

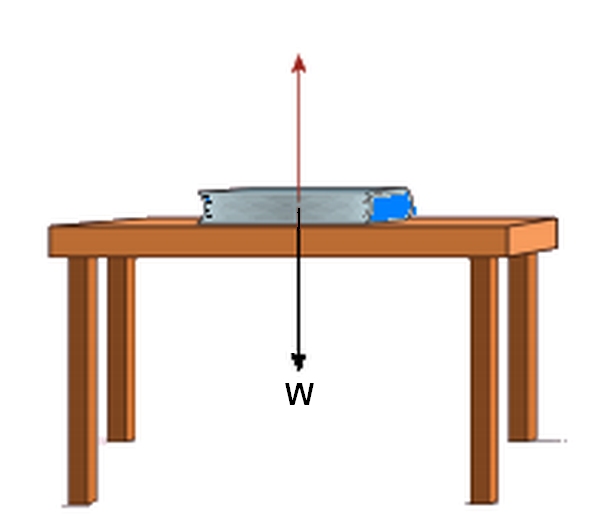
This action force - Weight and reaction force - Normal reaction force is an example of Newton's third law which states:
For every force there is an equal and opposite reaction force

Motion in Space

How does a rocket move in space since it has nothing to push against? This was a problem that politicians tried to answer at the start of the space race in order to justify the spending of vast sums of public money. Scientists were able to answer this question by referring to Newton's Third Law. When a rocket ejects hot exhaust gases from its engine the force of the hot gases leaving the rocket is matched by the reaction force of the gases on the rocket. Because the exhaust gases head downwards, they exert an equal and opposite force upwards on the rocket. It is this action-reaction force pair that allows the rocket to move through the vacuum of space. It does not need anything to push against, because the exhaust gases are pushing against the rocket.

---

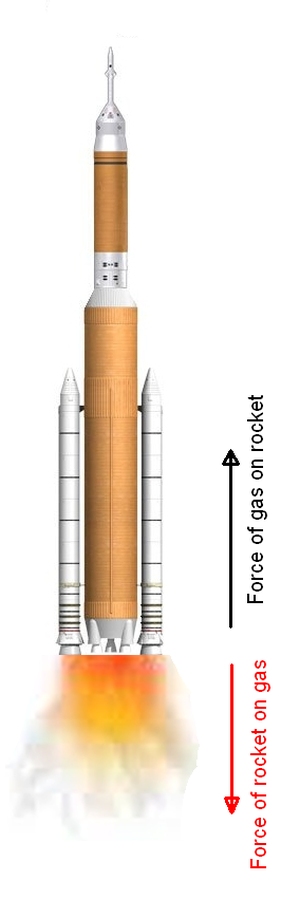
Force and acceleration

Attempt to solve the question yourself before clicking the solve button!

A rocket with a mass of kg. The rocket engines generate a thrust force of N. How fast does the rocket accelerate when lifting off?

---

Freefall and Terminal Velocity

When a skydiver jumps out of a plane they start to fall towards the ground. In the initial moments of the flight they are in freefall because the only force acting upon them is the gravitational force from the planet. Here on Earth the skydiver begins to experience the wind rushing past them as the accelerate towards the ground. As the skydiver travels faster they are having to push more air out of their way in each second. This air resists being pushed away and provides what is called air resistance. Eventually at about 120 mph/190 kph the force provided by the air resistance is equal to the graavitational force of the Earth. At this point the skydiver stops accelerating, but continues to fall to the ground at 120 mph/190 kph. This speed is called the terminal velocity. From this we can see that air resistance increases as speed increases. When the skydiver opens their parachute there is a greater air resistance force than gravitational force. The skydiver slows down. As they slow down the air resistance reduces until it is once again the same size as the gravitational force. At this point, with a new much slower speed the skydiver is not accelerating, but continues to fall to the ground at a constant speed until they land. This new slower speed is also a terminal velocity. Below is a graph showing the various stages. Note that throughout the time the skydiver is falling that the gravitational force does not change. The air resistance force changes until terminal velocity is reached and then it remains constant.

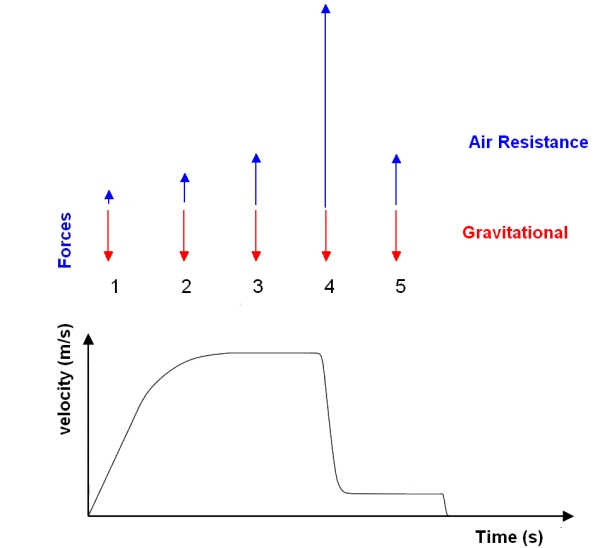
1. Skydiver accelerating rapidly at the start of the jump due to very small air resistance
2. Skydiver accelerating more slowly because of increased air resistance
3. Skydiver falling with constant speed - at terminal velocity - air resistance is the same size as the gravitational force
4. Skydiver opens parachute and air resistance increases dramatically
5. Skydiver is at new slower terminal velocity before hitting ground . The air resistance has reduced to the level of the gravitational force

In zones 1,2 and 4 the forces are unbalanced, therfore there is an acceleration.
In zones 3 and 5 the forces are balanced and so the skydiver falls at a constant speed.

On the moon any astronaut would remain in freefall down to the surface of the moon because there is no atmosphere. Therefore a parachute would not help to slow their acceleration to the surface either.