National 5 Physics

Projectile Motion

When a ball rolls off a table it is possible to model its motion. Scientists have discovered that the motion should be separated into two distinct motions.

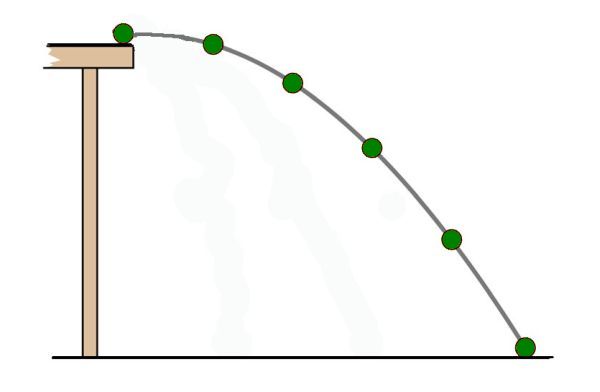
The two motions are at 90° to each other.

Horizontal motion

The horizontal motion of the ball is simply described as a constant velocity. This is true when the effects of air resistance can be ignored. In most situations set in Nat 5 questions this simplification is accepted. Over the measurements made at this level the assumption of constant velocity works very well.

Vertical motion

For all objects in a gravitational field when they are falling they will accelerate due to the gravitational field. The acceleration on Earth is 9.8 m/s². In the diagram below we can see the same ball launched at three different horizontal speeds off the table. v₁ is the slowest and v₃ is the fastest.

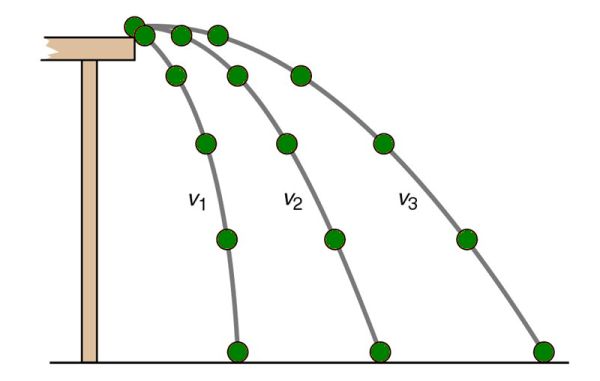
The diagram shows that the distance the ball falls vertically does not depend on the horizontal speed. It is only affected by the gravitational acceleration.

Example

A child throws a stone horizontally from a bridge into a river.

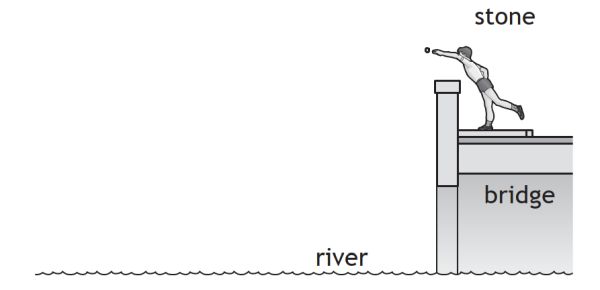
(a) On the above diagram sketch the path taken by the stone between leaving the child's hand and hitting the water.

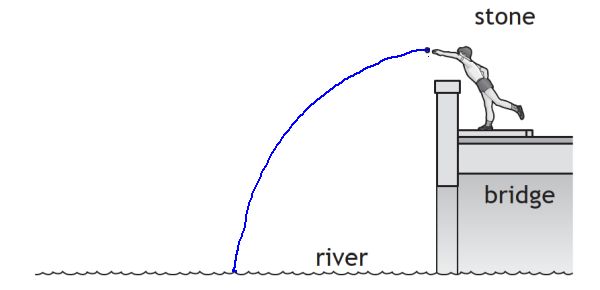
(b) The stone reaches the water 0.80 s after it was released.
  (i) Calculate the vertical velocity of the stone as it reaches the water. The effects of air resistance can be ignored.

The question is only asking about the vertical velocity. The initial vertical velocity is zero since the stone was thrown horizontally. Accelation is due to the gravitational field which is 9.8 m/s².
v = ?
u = 0 m/s
t = 0.80 s
a = 9.8 m/s²

v = u + at
v = 0 + 0.80 × 9.8
v = 7.8 m/s

(ii) Determine the height above the water at which the stone was released.

To solve this problem we must use the average speed of the falling ball. This can be found out using the equation:

$$\bar{v}=\frac{\mathrm{(v\; +\; u)}}{2}$$
d = ?
v = 3.9 m/s
t = 0.80 s

$$d=\bar{v}t$$ $$d=\mathrm{3.9 \times 0.80}$$

d = 3.1 m

  (iii)The boy threw the stone with a horizontal speed of 1.5 m/s. How far from the bridge did it land?

$$s=v_{h}t$$ $$s=\mathrm{1.5 \times 0.80}$$

s = 1.2 m

---

Interactive projectile motion question with solution

Attempt to solve the question yourself before clicking the solve button!

A ball is rolling off a horizontal table with a speed of m s^-1. It takes seconds to land on the floor.
(a) What vertical velocity did the ball hit the floor?
(b) What is the height of the table?
(c) How far from the table did the ball land?

---

Graphical Representation

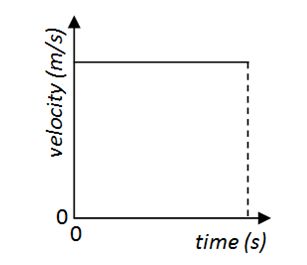
It is possible to use velocity time graphs to find out information on problems with projectile motion. The horizontal motion is a constant and so the graph will look like the one below:

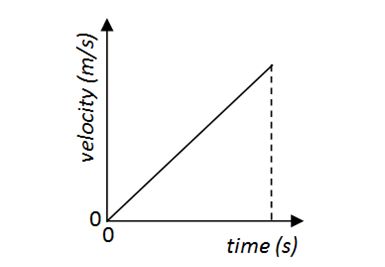
The vertical motion experiences a constant acceleration and so the graph produced would look like:

Calculating the area under each graph will give the distance travelled horizontally and vertically respectively.
Note that for the horizontal direction the area is simply speed × time
Note that for the vertical direction the area is simply the area of a triangle (1/2 × base × height)

Satellites and Orbital Motion

Imagine firing a projectile from a very high mountain. Start off with a low firing speed and then increase it. As the speed of the projectile increases so does its range. (The range is the horizontal distance to the cannonball landing from the point of firing). Eventually the speed might be fast enough for the projectile to reach all the way round the Earth. See the diagram below from IoP Spark

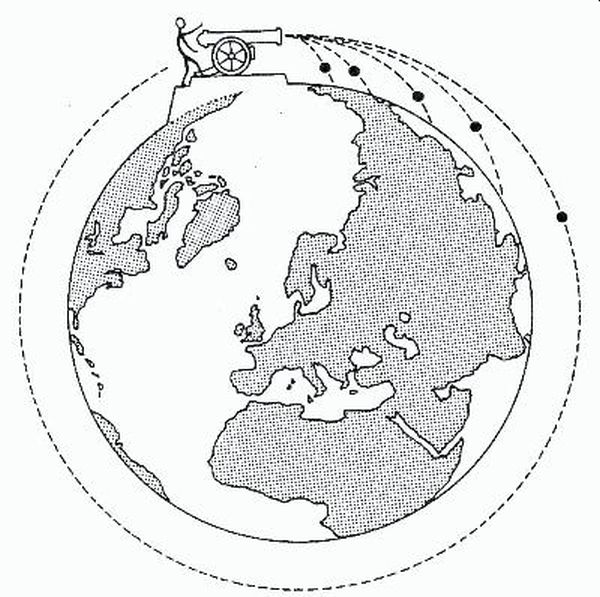
When thinking about orbital motion there is the forward horizontal motion of the object. This is around 7,800 m s^-1 for a satellite in low Earth orbit. The weight of the object means that the satellite is being pulled towards the centre of the Earth. The satellite is in a zero friction environment and so there is no air resistance. The speed of forward motion results in the gravitatonal acceleration producing a circular path around the Earth. This is similar to the thought experiment above with the cannonball.